Abstract
In Chapter 3 a number of methods were described for generating a phase-only hologram of an object. However, these methods are not applicable if the source image of the object is not present, and only its hologram is available. Such a situation happens if a hologram is directly captured from a physical object (for example applying phase-shifting holography), instead of generated from a numerical graphic model. This chapter describes six methods for converting a complex-valued hologram into a phase-only hologram. The first two methods, complex amplitude modulation (CAM) and double-phase methods, convert a complex-valued hologram into a pure phase representation. When the latter is displayed on an SLM with suitable optical filtering, a visual 3-D image is reconstructed. The third to fifth methods apply different variants of the Floyd–Steinberg error diffusion algorithm to convert a complex-valued hologram into a continuous tone phase-only hologram. Among these three error diffusion methods, bi-directional error diffusion results in the best reconstructed image, while the local error diffusion method can be implemented with parallel computing devices such as GPUs. The last method, known as direct binary search (DBS), converts a complex-valued hologram into a binary phase-only hologram through an iterative process. The quality of the reconstructed image is generally poor unless more iterations are performed at the expense of longer computation time. A phase-only hologram generated by error diffusion or DBS can be displayed directly with a phase-only SLM without additional optical processing.
4.1 Introduction
In previous chapters, different methods for generating a phase-only hologram for a given 3-D object, such as the iterative Fresnel transform algorithm (IFTA), downsampling, and the patterned phase method, have been presented. While all these methods are effective in generating phase-only holograms, they all share the same prerequisite that a source image has to be available in the first place. This is not a problem in computer-generated holography (CGH), in which case the source images are provided in the form of numerical data, such as point cloud files or computer graphic models. However, in some applications such as remote sensing and microscopic holography, a hologram is captured directly from a real object based on acquisition methods like optical scanning holography and phase-shifting holography. For these cases, the source image is not available, and the methods that have been gone through previously are not applicable for deriving the phase-only hologram.
Intuitively, it could be possible to reconstruct the 3-D source image from a complex-valued hologram, with which a phase-only hologram can be generated with IFTA or other methods. However, there is a lack of an effective method that can reconstruct an arbitrary 3-D image from its hologram. In most of the methods developed to date, a hologram is reconstructed onto a series of regularly spaced depth planes. Subsequently, some sort of sharpness or focus index is measured for each region on the stack of reconstructed images, and the depth plane with the sharpest measurement among all its peers will be taken to be the focused plane of that particular region. Although such an approach is logical and quite sound, existing hologram reconstruction methods such as those discussed in [1–4] are computation intensive, and so only of use for reconstructing simple geometries. For more complicated object shapes, a region is likely to contain contents with a wider range of depths. When one area within a region is in focus, the remaining part may become blurred and the out-of-focus content may blend into the neighboring focused region(s). It is therefore not possible to use the sharpness index to locate the focused plane of each region unless the object space is thin or comprises of widely separated items.
Alternatively, it is possible to convert a complex-valued hologram into a phase-only hologram. There are two major difficulties with this approach. First, the process is lossy and irreversible, as the magnitude component of the hologram is removed. The amount of distortion incurred in the conversion is unpredictable. Second, as there is no information on the source image that is represented by the hologram, iterative techniques (for example, the Gerchberg–Saxton algorithm) cannot be applied to minimize the conversion error. This chapter describes six methods for converting a complex-valued hologram into a phase-only hologram: complex amplitude modulation (CAM); double-phase decomposition; uni-directional error diffusion (UERD); bi-directional error diffusion (BERD); localized error diffusion (LERD); and direct binary search (DBS). This last method is used for obtaining a binary phase-only hologram from the complex-valued hologram.
4.2 Complex Amplitude Modulation
Complex amplitude modulation is a method of encoding both the amplitude and phase components of a complex-valued function into a phase-only function. The idea of applying this concept in digital holography could be dated back to 1999, when J.A. Davis and his team succeeded in implementing phase-only optical filters for optical recognition and image processing [5]. Recently, the method has been applied to convert a complex-valued hologram into a phase-only hologram [6,7]. Upon illumination with a reference beam and filtering of the diffracted waves, the source image recorded in the phase-only hologram will be reconstructed as a visible image.
Here, a complex-valued hologram H(m,n)=|H(m,n)|expiθ(m,n)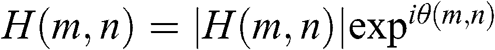 is to be converted into a phase-only hologram Hp(m,n)
is to be converted into a phase-only hologram Hp(m,n)![]() . After the hologram is generated, it will be illuminated by an inclined plane wave R(m,n)=|R(m,n)|expiθR(m,n)
. After the hologram is generated, it will be illuminated by an inclined plane wave R(m,n)=|R(m,n)|expiθR(m,n)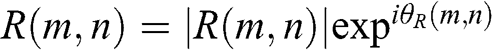 , making an angle of incidence θR along the vertical or horizontal direction for reconstructing the image recorded in the hologram.
, making an angle of incidence θR along the vertical or horizontal direction for reconstructing the image recorded in the hologram.
Converting the hologram into a phase-only hologram with CAM is straightforward. The phase-only hologram is obtained simply by integrating the hologram H(m,n)![]() and the off-axis plane wave into a phase function:
and the off-axis plane wave into a phase function:
 (4.1)
(4.1) where c and β![]() are constant terms.
are constant terms.
To view the reconstructed image, the phase-only hologram HP(m,n)![]() is illuminated by the inclined reference plane wave R(m,n)
is illuminated by the inclined reference plane wave R(m,n)![]() that is making an angle of incidence θR along the vertical or horizontal direction. The diffracted wave on the reconstructed image plane is
that is making an angle of incidence θR along the vertical or horizontal direction. The diffracted wave on the reconstructed image plane is
 (4.2)
(4.2) From Eq. (4.2) it can be seen that although the expression should contain the signal corresponding to the hologram H(m,n)![]() , the diffracted wave DP(m,n)
, the diffracted wave DP(m,n)![]() also includes components that are different from the hologram. The question is: How can the hologram signal H(m,n)
also includes components that are different from the hologram. The question is: How can the hologram signal H(m,n)![]() be separated from the rest of the terms in DP(m,n)
be separated from the rest of the terms in DP(m,n)![]() . It is shown in [6] that this is achieved by decomposing the expression in Eq. (4.2) into an infinite series based on the following property of the Bessel function:
. It is shown in [6] that this is achieved by decomposing the expression in Eq. (4.2) into an infinite series based on the following property of the Bessel function:
 (4.3)
(4.3) where Jk(s)![]() is the kth order of the Bessel function of the first kind.
is the kth order of the Bessel function of the first kind.
Applying Eq. (4.3) to Eq. (4.2), the diffraction wave DP(m,n)![]() is the sum of an infinite series of functions:
is the sum of an infinite series of functions:
 (4.4)
(4.4) Eq. (4.4) is equivalent to the superposition of an infinite number of off-axis holograms; the reconstructed image of each one projects at a unique angle, which is an integer multiple of the off-axis illumination angle θR of the reference plane wave. For simplicity, the constant term c can be taken as unity.
In Eq. (4.4), the component corresponding to k=−1![]() ,
,
 (4.5)
(4.5) The reconstructed images of higher-order diffraction with |k|>1![]() should be non-overlapping with the one corresponding to k=−1
should be non-overlapping with the one corresponding to k=−1![]() if the angle of incidence θR of the reference wave is sufficiently large. Based on this assumption, an optical mask can be applied to extract HCAM(m,n)
if the angle of incidence θR of the reference wave is sufficiently large. Based on this assumption, an optical mask can be applied to extract HCAM(m,n)![]() from the rest of the unwanted components. From Eq. (4.5), the −1 order of diffraction (denoted by HCAM(m,n)
from the rest of the unwanted components. From Eq. (4.5), the −1 order of diffraction (denoted by HCAM(m,n)![]() ) is related to the complex amplitude distribution of the hologram H(m,n)
) is related to the complex amplitude distribution of the hologram H(m,n)![]() . If J−1[|H(m,n)|]
. If J−1[|H(m,n)|]![]() is similar to H(m,n)
is similar to H(m,n)![]() , the source image can be reconstructed to a good approximation from this component. The reconstructed image of HCAM(m,n)
, the source image can be reconstructed to a good approximation from this component. The reconstructed image of HCAM(m,n)![]() will carry a certain amount of distortion, as the hologram has been changed to the function J−1[|H(m,n)|]
will carry a certain amount of distortion, as the hologram has been changed to the function J−1[|H(m,n)|]![]() , and the reconstructed image is overlaid with the zero-order ( k=0
, and the reconstructed image is overlaid with the zero-order ( k=0![]() ).
).
The first type of distortion, resulting from the modification of the hologram by J−1[|H(m,n)|]![]() , can be alleviated by selecting a value for the constant term β
, can be alleviated by selecting a value for the constant term β![]() that restricts the dynamic range of |H(m,n)|
that restricts the dynamic range of |H(m,n)|![]() to the linear region of the Bessel function. To illustrate this point, a plot of the function J−1[x]
to the linear region of the Bessel function. To illustrate this point, a plot of the function J−1[x]![]() for x=[0,5]
for x=[0,5]![]() is shown in Figure 4.1. From the diagram, the Bessel function is close to a linear function for x within the range [0,1.5].
is shown in Figure 4.1. From the diagram, the Bessel function is close to a linear function for x within the range [0,1.5].
The distortion caused by the overlaying of the zero-order component on the reconstructed image can be removed with an optical filter formed by a pair of lens arranged in a 4f filtering configuration.
Numerical simulation of the CAM method is conducted using the MATLAB code provided in Section 4.8.1. A complex-valued Fresnel hologram of the source image “Apple” in Figure 4.2(a) is first generated. Next, the phase-only hologram corresponding to the −1 order of diffraction signal HCAM(m,n)![]() is extracted with Eq. (4.5). A reconstructed image of the phase-only hologram on the focused plane is thus obtained. The reconstructed images corresponding to β
is extracted with Eq. (4.5). A reconstructed image of the phase-only hologram on the focused plane is thus obtained. The reconstructed images corresponding to β![]() = 3.0, 2.0, and 0.50 are shown in Figures 4.2(b–d). In all these images, the dynamic range of brightness has been normalized to the range {0,255}
= 3.0, 2.0, and 0.50 are shown in Figures 4.2(b–d). In all these images, the dynamic range of brightness has been normalized to the range {0,255}![]() , with 0 and 255 representing the lowest and the highest intensities, respectively. The attenuation of the brightness due to β
, with 0 and 255 representing the lowest and the highest intensities, respectively. The attenuation of the brightness due to β![]() , therefore, is not shown in the figures. The fidelities of the three reconstructed images, as compared with the original one in Figure 4.2(a), are 14.45 dB, 20.89 dB, and 30 dB for β=3
, therefore, is not shown in the figures. The fidelities of the three reconstructed images, as compared with the original one in Figure 4.2(a), are 14.45 dB, 20.89 dB, and 30 dB for β=3![]() , β=2
, β=2![]() , and β=0.5
, and β=0.5![]() . In general, the larger the peak-signal-to-noise-ratio (PSNR), the higher is the fidelity of the image. By observation, the quality of the reconstructed image is increased with decreasing values of β
. In general, the larger the peak-signal-to-noise-ratio (PSNR), the higher is the fidelity of the image. By observation, the quality of the reconstructed image is increased with decreasing values of β![]() , which is also reflected by the increase in PSNR. However, from Eq. (4.5) and Figure 4.1, the smaller the value of β
, which is also reflected by the increase in PSNR. However, from Eq. (4.5) and Figure 4.1, the smaller the value of β![]() , the weaker the magnitude of the hologram HCAM(m,n)
, the weaker the magnitude of the hologram HCAM(m,n)![]() , and the dimmer will be its reconstructed image. Hence it is necessary to find a value of β
, and the dimmer will be its reconstructed image. Hence it is necessary to find a value of β![]() that results in a reconstructed image with higher fidelity and sufficient brightness to create a favorable visual quality.
that results in a reconstructed image with higher fidelity and sufficient brightness to create a favorable visual quality.
Figure 4.2 (a) Source image “Apple.” (b–d) Reconstructed image from HCAM(m, n) with β = 3, 2, 0.5, respectively.
Another similar simulation is applied to convert the complex-valued hologram of the double-depth image “HK1” in Figure 1.12 into a phase-only hologram with the CAM method. The source image is divided into left and right sections located at axial distances of z1=0.07 m![]() and z2=0.08 m
and z2=0.08 m![]() from the hologram. A phase-only hologram is generated with β=0.5
from the hologram. A phase-only hologram is generated with β=0.5![]() , and the reconstructed images at the two focused planes are shown in Figure 4.3. From these two images, each side of the source image is reconstructed as a sharp image on its focused plane, with the other side being a blurred, defocused image. This simulation result demonstrates that the CAM method is capable of generating a phase-only hologram that can represent both intensity and depth dimension.
, and the reconstructed images at the two focused planes are shown in Figure 4.3. From these two images, each side of the source image is reconstructed as a sharp image on its focused plane, with the other side being a blurred, defocused image. This simulation result demonstrates that the CAM method is capable of generating a phase-only hologram that can represent both intensity and depth dimension.
4.3 Double-Phase Macro-Pixel Hologram
The double-phase macro-pixel hologram is based on the principle that if a complex number is bounded within the unit circle, it can be represented as the sum of two phase-only quantities. As a result, any complex quantity can be converted into a pure phase representation. Mathematically, given a complex number A expiθ![]() with A within the range [0,1], the sum of two phase terms is expressed as
with A within the range [0,1], the sum of two phase terms is expressed as
 (4.6)
(4.6) where A=cos(α)![]() , θ1=θ+α
, θ1=θ+α![]() , and θ2=θ−α
, and θ2=θ−α![]() . The simple mathematical relation in Eq. (4.6) suggests that this principle can be applied to convert a complex-valued hologram into a pair of phase-only images, which could be integrated in certain ways to form a double-phase-only hologram (DPH). From Eq. (4.6), it can be seen that as A
. The simple mathematical relation in Eq. (4.6) suggests that this principle can be applied to convert a complex-valued hologram into a pair of phase-only images, which could be integrated in certain ways to form a double-phase-only hologram (DPH). From Eq. (4.6), it can be seen that as A![]() is positive, the angle α=cos−1(A)
is positive, the angle α=cos−1(A)![]() is confined to the right half of the Euclidean plane.
is confined to the right half of the Euclidean plane.
The generation of a double-phase hologram was achieved by the pioneering attempt of C. Hsueh and A. Sawchuk [8] in the mid-1970s. In their investigation, a Fourier hologram was decomposed into a pair of phase components based on Eq. (4.6). Next, each Fourier cell (which can be interpreted as a hologram pixel) was split into two sub-cells, each encoding one of the phase terms. In the simplest case, a Fourier cell is evenly separated into two partitions, as shown in Figure 4.4(a). In each partition, a window of half the length of the cell is shifted vertically by an amount ( τ1![]() or τ2
or τ2![]() ), which is proportionally to the phase quantity it represents.
), which is proportionally to the phase quantity it represents.
Figure 4.4 (a) A Fourier cell with two vertical shifted sub-cells for representing two phase quantities. (b) Interleaving a pair of phase components with the 1 × 2 macro-pixel topology. (c) Interleaving a pair of phase components with the 2 × 2 macro-pixel topology.
With the availability of electronic accessible phase-only spatial light modulators (SLMs), the display of DPH has been simplified. In the work of J.M. Florence and R.D. Juday [9], a complex-valued Fresnel hologram H(m,n)![]() was decomposed into a pair of phase-only images, θ1(m,n)
was decomposed into a pair of phase-only images, θ1(m,n)![]() and θ2(m,n)
and θ2(m,n)![]() :
:
 (4.7)
(4.7) Although both exponential terms on the right-hand side of Eq. (4.7) are phase-only quantities with constant magnitude of unity, they have to be combined to the complex-valued hologram. To address this issue, the two phase images are combined into a double-phase hologram θM(m,n)![]() through spatial interleaving. A straightforward way to interleave the pair of phase images is to copying the odd and even rows of θ1(m,n)
through spatial interleaving. A straightforward way to interleave the pair of phase images is to copying the odd and even rows of θ1(m,n)![]() and θ2(m,n)
and θ2(m,n)![]() to the odd and even rows of θM(m,n)
to the odd and even rows of θM(m,n)![]() , respectively. The adjacent pair of pixels in θM(m,n)
, respectively. The adjacent pair of pixels in θM(m,n)![]() forms a 1×2
forms a 1×2![]() macro-pixel, with each of its element (referred to as a sub-pixel) contributing from either θ1(m,n)
macro-pixel, with each of its element (referred to as a sub-pixel) contributing from either θ1(m,n)![]() or θ2(m,n)
or θ2(m,n)![]() , as shown in Figure 4.4(b). In another words, the pair of phase images are each downsampled by two times and placed at non-overlapping areas in θM(m,n)
, as shown in Figure 4.4(b). In another words, the pair of phase images are each downsampled by two times and placed at non-overlapping areas in θM(m,n)![]() .
.
When the double-phase hologram is illuminated by a coherent beam, the diffracted waves corresponding to θ1(m,n)![]() and θ2(m,n)
and θ2(m,n)![]() will be generated and merged on the reconstruction plane. However, due to the downsampling of these two signals, their frequency spectra will be added with aliasing images. In order to attenuate the aliasing images, and to merge θ1(m,n)
will be generated and merged on the reconstruction plane. However, due to the downsampling of these two signals, their frequency spectra will be added with aliasing images. In order to attenuate the aliasing images, and to merge θ1(m,n)![]() and θ2(m,n),
and θ2(m,n),![]() certain optical filtering or processing has to be applied so that the reconstructed image will be similar to that of the original hologram H(m,n)
certain optical filtering or processing has to be applied so that the reconstructed image will be similar to that of the original hologram H(m,n)![]() . As pointed out by V. Arrizón and D. Sanchez-de-la-Llave [10], the region in the reconstruction plane having high fidelity (measured in terms of signal-to-noise ratio) is rather small along the direction of the macro-pixel. To enhance the fidelity, the symmetrical 2×2
. As pointed out by V. Arrizón and D. Sanchez-de-la-Llave [10], the region in the reconstruction plane having high fidelity (measured in terms of signal-to-noise ratio) is rather small along the direction of the macro-pixel. To enhance the fidelity, the symmetrical 2×2![]() distribution of sub-pixels in Figure 4.4(c) is often adopted in forming a macro-pixel.
distribution of sub-pixels in Figure 4.4(c) is often adopted in forming a macro-pixel.
In the 2×2![]() macro-pixel arrangement, the pair of phase components θ1(m,n)
macro-pixel arrangement, the pair of phase components θ1(m,n)![]() and θ2(m,n)
and θ2(m,n)![]() are downsampled by the orthogonal uniform sampling lattices L1(m,n)
are downsampled by the orthogonal uniform sampling lattices L1(m,n)![]() and L2(m,n)
and L2(m,n)![]() , as shown in Figure 4.5(a) and 4.5(b). Each lattice is in the form of a checkerboard pattern, with the sampled and non-sampled points assigned values of 1 (white) and 0 (black), respectively. The result of multiplexing θ1(m,n)
, as shown in Figure 4.5(a) and 4.5(b). Each lattice is in the form of a checkerboard pattern, with the sampled and non-sampled points assigned values of 1 (white) and 0 (black), respectively. The result of multiplexing θ1(m,n)![]() and θ2(m,n)
and θ2(m,n)![]() with the two sampling lattices is shown in Figure 4.5(c):
with the two sampling lattices is shown in Figure 4.5(c):
Figure 4.5 (a) Sampling lattice L1(m, n). (b) Sampling lattice L2(m, n). (c) Multiplexing θ1(m, n) and θ2(m, n) with L1(m, n) and L2(m, n).
The Fourier transform of θM(m,n)![]() is given by
is given by
where B˜(ωm,ωn)![]() denotes the Fourier transform of an arbitrary function B(m,n)
denotes the Fourier transform of an arbitrary function B(m,n)![]() , and ∗
, and ∗![]() is the convolution operator. Eq. (4.9) is therefore rewritten as
is the convolution operator. Eq. (4.9) is therefore rewritten as
 (4.10)
(4.10) The first term on the right-hand side of Eq. (4.10) is the Fourier transform of the original hologram H(m,n)![]() , while the rest of the terms are aliasing components comprising of shifted replicas of the baseband signal. If the sampling interval is small enough, the aliasing components are widely spaced so that they could be suppressed to a large extent with a low-pass filter. For example, an optical filter realized with a standard 4f configuration and an iris around the center of the Fourier plane can be employed to extract a low-pass version HL(m,n)
, while the rest of the terms are aliasing components comprising of shifted replicas of the baseband signal. If the sampling interval is small enough, the aliasing components are widely spaced so that they could be suppressed to a large extent with a low-pass filter. For example, an optical filter realized with a standard 4f configuration and an iris around the center of the Fourier plane can be employed to extract a low-pass version HL(m,n)![]() of the original complex hologram signal.
of the original complex hologram signal.
Numerical simulation on the double-phase macroblock method in converting a complex-valued hologram into a phase-only hologram is conducted with the MATLAB code in Section 4.8.2. First, a complex-valued hologram is generated for the double-depth image “HK1” in Figure 1.12. Next, the complex-valued hologram is converted into a pair of phase-only holograms with the double-phase macroblock method, based on the 1×2![]() and the 2×2
and the 2×2![]() macroblock topologies. Subsequently, each phase-only hologram is low-pass filtered with the bandwidth limited to one-quarter of its original value, so that aliasing errors at the high frequency range are suppressed. The reconstructed images at the two focused planes of the phase holograms generated with the 1×2
macroblock topologies. Subsequently, each phase-only hologram is low-pass filtered with the bandwidth limited to one-quarter of its original value, so that aliasing errors at the high frequency range are suppressed. The reconstructed images at the two focused planes of the phase holograms generated with the 1×2![]() topology and the 2×2
topology and the 2×2![]() macroblock topologies are shown in Figures 4.6(a, b) and 4.6(c, d), respectively.
macroblock topologies are shown in Figures 4.6(a, b) and 4.6(c, d), respectively.
Figure 4.6 Reconstructed images on the two focused planes from the low-pass double-phase hologram: (a) 1 × 2 macro-pixel topology, focused plane at 0.07 m; (b) 1 × 2 macro-pixel topology, focused plane at 0.08 m; (c) 2 × 2 macro-pixel topology, focused plane at 0.07 m; (d) 2 × 2 macro-pixel topology, focused plane at 0.08 m.
First we inspect the reconstructed images in Figure 4.6(a, b) of the double-phase hologram that has been interleaved with the 1×2![]() macro-pixel topology. Each side of the image is reconstructed clearly from the hologram on its corresponding focused plane. However, the images are quite heavily contaminated with noise. In the reconstructed images in Figure 4.6(c, d), which are derived from the double-phase hologram interleaved with the 2×2
macro-pixel topology. Each side of the image is reconstructed clearly from the hologram on its corresponding focused plane. However, the images are quite heavily contaminated with noise. In the reconstructed images in Figure 4.6(c, d), which are derived from the double-phase hologram interleaved with the 2×2![]() topology, the noise is not prominent. These results show that the 2×2
topology, the noise is not prominent. These results show that the 2×2![]() interleaving method is preferable in the generation of the double-phase hologram.
interleaving method is preferable in the generation of the double-phase hologram.
4.4 Uni-directional Error Diffusion
Although the CAM method and the double-phase hologram are both effective in converting a complex-valued Fresnel hologram into a phase-only hologram, some optical accessories (such as an optical mask and optical filter) are required to suppress the unwanted signals in the display process. This will lead to greater complexity, size, and cost of the display systems, imposing limitations on practical applications. Recently, P. Tsang and T.-C. Poon have proposed employing error diffusion for converting a Fresnel hologram into a phase-only hologram. A phase-only hologram derived with this method is referred to as a uni-directional error diffusion (UERD) hologram [11]. There are two major advantages of the UERD hologram. First, the computation time that is required to convert a complex-valued hologram to a phase-only hologram is short. Second, the phase-only hologram obtained with the UERD method can be optically reconstructed simply by illuminating the hologram with a coherent beam without additional optical processing.
Error diffusion is a technique that was originally developed for quantizing pixels of a continuous tone image with a small number of quantization levels. It has been widely applied for many decades in facsimile transmission and printing, where most of the equipment can only print binary images comprising pixels of either black or white. In general, the visual quality of a binary image that is converted with error diffusion from a continuous tone image, is preserved favorably. There are many variations in the error diffusion algorithm, the most notable one being perhaps the Floyd–Steinberg algorithm [12]. In this approach, the pixels in an image are processed sequentially in a row-by-row, left-to-right manner. Each visited pixel will be changed to a white pixel if its intensity exceeds a certain threshold, and changed to a black pixel otherwise. The error resulting from the bi-level quantization is distributed, with predefined proportions, to the four adjacent neighbors of the pixel. As the direction of processing the pixels is identical in each row, this is referred to as uni-directional error diffusion.
In [11], the principles of the Floyd–Steinberg error diffusion technique is applied to obtain the phase-only hologram. Given a complex-valued Fresnel H(m,n)![]() with the dynamic range of the magnitude normalized to [0,1], each pixel is scanned sequentially in a row-by-row, left-to-right manner. The magnitude of the pixel under evaluation is forced to unity, resulting in a phase-only component, and the error is computed and distributed to its four immediate neighbors. The process is repeated until all the pixels have been converted into a phase-only hologram HP(m,n)
with the dynamic range of the magnitude normalized to [0,1], each pixel is scanned sequentially in a row-by-row, left-to-right manner. The magnitude of the pixel under evaluation is forced to unity, resulting in a phase-only component, and the error is computed and distributed to its four immediate neighbors. The process is repeated until all the pixels have been converted into a phase-only hologram HP(m,n)![]() .
.
Suppose Pmj;nj![]() denotes the current pixel that is being visited at (mj,nj)
denotes the current pixel that is being visited at (mj,nj)![]() ; the error that results from forcing its magnitude to unity will be
; the error that results from forcing its magnitude to unity will be
The error E(mj,nj)![]() is then added, with preset weighting factors, to the four adjacent pixels that have not been visited yet, as shown in Figure 4.7.
is then added, with preset weighting factors, to the four adjacent pixels that have not been visited yet, as shown in Figure 4.7.
Figure 4.7 Diffusion of error in the current hologram pixel to its four immediate neighbors.
Mathematically, the values of these four pixels will be updated according to the following equations:
where B← A denotes replacing the value of B with the value of A. In [11], the weighting factors w1![]() to w3
to w3![]() follow the values adopted in the original Floyd–Steinberg algorithm, with w1=716
follow the values adopted in the original Floyd–Steinberg algorithm, with w1=716 , w2=316
, w2=316 , w3=516
, w3=516 , and w4=116
, and w4=116 . Optimizing the weighting factors for further enhancing the fidelity of the reconstructed image of the phase-only hologram was attempted in [13].
. Optimizing the weighting factors for further enhancing the fidelity of the reconstructed image of the phase-only hologram was attempted in [13].
It can be seen from the above equations that error diffusion is a recursive process whereby pixels are processed sequentially, and non-visited pixels are modified by the errors imparted from those that have been processed. Compared with the CAM and the double-phase method, error diffusion requires a greater amount of computation, and its recursive nature prohibits the use of parallel computation. However, an error diffusion hologram can be displayed directly by illuminating it with a coherent beam, and no other optical accessories such as optical filtering and masking are required.
Numerical simulation of the UERD method is conducted with the MATLAB codes in Section 4.8.3. In the simulation, a complex-valued Fresnel hologram H(m,n)![]() of the double-depth source image “HK1” is first generated. Next, Eqs. (4.12)–(4.15) are applied to convert H(m,n)
of the double-depth source image “HK1” is first generated. Next, Eqs. (4.12)–(4.15) are applied to convert H(m,n)![]() into a phase-only hologram HP(m,n)
into a phase-only hologram HP(m,n)![]() . Finally, the left and the right sides of the phase-only hologram are each reconstructed with Fresnel diffraction on its corresponding focused plane. The reconstructed images are displayed and shown in Figure 4.8. It can be observed that apart from some noise contamination, the reconstructed image is similar to the original one. The CPU time taken in the error diffusion, based on a typical PC, is around 36 s.
. Finally, the left and the right sides of the phase-only hologram are each reconstructed with Fresnel diffraction on its corresponding focused plane. The reconstructed images are displayed and shown in Figure 4.8. It can be observed that apart from some noise contamination, the reconstructed image is similar to the original one. The CPU time taken in the error diffusion, based on a typical PC, is around 36 s.
Figure 4.8 Reconstructed image from the UERD hologram: (a) on focused plane at 0.07 m; (b) on focused plane at 0.08 m.
4.5 Bi-directional Error Diffusion
In the conversion of a complex-valued hologram to a phase-only hologram with UERD, the error that is caused by discarding the magnitude component of each hologram pixel is diffused to the pixel at its right and the three pixels underneath. The accumulated error EACC(mj,nj)![]() received by a pixel at location (mj,nj)
received by a pixel at location (mj,nj)![]() can be calculated with a recursive process:
can be calculated with a recursive process:
 (4.16)
(4.16) Eq. (4.16) infers that the errors are propagating, and to a certain extent accumulating along the down-diagonal direction. This has the effect of errors being correlated along the line of propagation and becoming less separable from the signal. The bi-directional error diffusion (BERD) [11] is a method to break the directional behavior of error propagation, randomizing the probability distribution of the errors to make it less correlated with the signal.
Similar to UERD, pixels in a complex-valued hologram are visited in a row-by-row manner. For the even rows (i.e., rows 0, 2, 4, etc.), the pixels are scanned from left to the right, whereas pixels of the odd rows are scanned in the reverse direction. The magnitude of each visited pixel is set to unity, and the resulting error is diffused to its four immediate neighbors. The distribution of error from a pixel to its neighbors is identical to UERD for the even rows of pixels (i.e., the same as Figure 4.7). For the odd rows, the direction of scanning is reversed, and the distribution of error from the current pixel Pmj;nj![]() to the four neighboring pixels is given in following equations:
to the four neighboring pixels is given in following equations:
Numerical simulation on the BERD method is conducted with the MATLAB codes given in Section 4.8.4. In the simulation, a complex-valued Fresnel hologram H(m,n)![]() of the double-depth source image “HK1” is first generated. Next, Eqs. (4.17)–(4.20) are applied to convert H(m,n)
of the double-depth source image “HK1” is first generated. Next, Eqs. (4.17)–(4.20) are applied to convert H(m,n)![]() into a phase-only hologram HP(m,n)
into a phase-only hologram HP(m,n)![]() . Finally, the left and the right sides of the phase-only hologram are each reconstructed with Fresnel diffraction on its corresponding focused plane. The reconstructed images are displayed as shown in Figure 4.9. They show that the numerical reconstructed images are similar to the original one, and the noise contamination is less than that of the UERD hologram.
. Finally, the left and the right sides of the phase-only hologram are each reconstructed with Fresnel diffraction on its corresponding focused plane. The reconstructed images are displayed as shown in Figure 4.9. They show that the numerical reconstructed images are similar to the original one, and the noise contamination is less than that of the UERD hologram.
Figure 4.9 Reconstructed image from the BERD hologram: (a) on focused plane at 0.07 m; (b) on focused plane at 0.08 m.
Despite the high quality of the reconstructed image of an inline BERD or a UERD hologram, the optical reconstructed image is rather poor. One of the reasons is that the error diffusion process requires very precise compensation of the error in one pixel by its neighbors. While this can be resolved by numerical computation, it is not implementable in practice as the SLMs that are employed for holographic display are imperfect. Any deviation in the locations of the pixels in an SLM, or the error in modulating the phase of the optical waves passing through them, will offset the delicate error compensation mechanism of the error diffusion process. A second factor leading to the poor optical reconstruction is the error that is associated with each of the hologram pixels that cannot be fully removed with error diffusion. Grossly speaking, error diffusion is capable of reducing, but not eliminating, the error caused by discarding the magnitude component of a hologram. For an inline hologram, the zero-order beam, together with the optical waves of the error signals, will merge with the reconstructed image of the hologram, resulting in severe degradation of the visual quality.
A simple way of overcoming the abovementioned problem is to add an off-axis reference beam to convert the inline phase-only hologram into an off-axis hologram, so that the reconstructed image can be steered away from the zero-order beam and the error component. Mathematically, the off-axis phase-only hologram is presented as
where R(n)=ei2πλnδdsin(θR) represents an optical beam inclined at an angle of incidence θR
represents an optical beam inclined at an angle of incidence θR![]() along the vertical direction. Since both HP(m,n)
along the vertical direction. Since both HP(m,n)![]() and R(n)
and R(n)![]() are phase-only functions, HOA(m,n)
are phase-only functions, HOA(m,n)![]() is also a phase-only hologram.
is also a phase-only hologram.
4.6 Localized Error Diffusion
As mentioned in Section 4.5, error diffusion is a recursive process whereby the conversion of a hologram into a phase-only value has to wait for the conversion of all the pixels before it can be completed. The error diffusion process, therefore, cannot be speeded up with parallel processing, and operation at a video rate of 25–30 frames per second is difficult to attain. To overcome this problem, a fast algorithm known as “localized error diffusion” was suggested in [14]. Briefly, a hologram is evenly partitioned into vertical zones each comprising a fixed number of columns. In each zone, modified UERD, which is referred to as localized error diffusion (LERD), is applied to convert the hologram pixels to phase-only values. The LERD enables the error diffusion process in each zone to be conducted in a concurrent manner, so that it can be executed with fast parallel processors such as graphics processing units (GPUs). Details of the method are as follows.
Consider converting a complex-valued hologram H(m,n)![]() into a phase-only hologram. The hologram is uniformly partitioned into K vertical zones, each comprising N columns, as shown in Figure 4.10(a), and each zone is hereafter referred to as a sub-hologram Hk(m,n)|1≤k≤K
into a phase-only hologram. The hologram is uniformly partitioned into K vertical zones, each comprising N columns, as shown in Figure 4.10(a), and each zone is hereafter referred to as a sub-hologram Hk(m,n)|1≤k≤K![]() . Next, LERD is applied to convert each sub-hologram Hk(m,n)
. Next, LERD is applied to convert each sub-hologram Hk(m,n)![]() into a phase-only hologram Hp;k(m,n)
into a phase-only hologram Hp;k(m,n)![]() .
.
Figure 4.10 (a) Partitioning a hologram into vertical zones. (b) Diffusion of error for a pixel that is not in the last column of a sub-hologram. (c) Diffusion of error for a pixel at the last column of a sub-hologram.
Similar to the UERD algorithm in Section 4.4, each sub-hologram is processed in a row-by-row manner, progressing from the first row to the last row. In each row, which is referred to as a segment, pixels are scanned from left to right. The magnitude of each visited pixel in a segment is forced to unity, and the phase value is retained. Suppose Pmj;nj;k![]() denotes the pixel being visited at location (mj,nj)
denotes the pixel being visited at location (mj,nj)![]() in the kth sub-hologram, the error Ek(mj,nj)
in the kth sub-hologram, the error Ek(mj,nj)![]() resulting from forcing its magnitude to unity will be
resulting from forcing its magnitude to unity will be
The error Ek(mj,nj)![]() is then added, with preset weighting factors, to the pixels in its neighborhood. For pixels that are not located in the last column of a sub-hologram, the error is added to its four adjacent pixels as shown in Figure 4.10(b):
is then added, with preset weighting factors, to the pixels in its neighborhood. For pixels that are not located in the last column of a sub-hologram, the error is added to its four adjacent pixels as shown in Figure 4.10(b):
where w1![]() to w4
to w4![]() are the Floyd–Steinberg error diffusion coefficients.
are the Floyd–Steinberg error diffusion coefficients.
For pixels in the last column of a sub-hologram, the error is added to the three pixels in the next row, as shown in Figure 4.10(c). Mathematically this is denoted as
where w5=39 , w6=59
, w6=59 , and w7=19
, and w7=19 .
.
From Figure 4.10, as well as Eqs. (4.23)–(4.29), in the processing of each row of pixels in a sub-hologram, the error of any pixel in one zone will not propagate to the pixels of other zones on the same row. In another words, the computation performed on any sub-hologram on a given row does not rely on the outcome of other sub-holograms. As such, error diffusion can be conducted concurrently for all the segments in the same row of the sub-holograms, hence enabling parallel processors to be utilized to speed up the conversion process. Suppose the width of each segment is S![]() pixels, and N
pixels, and N![]() is the horizontal extent of the hologram, there will be N/S
is the horizontal extent of the hologram, there will be N/S![]() sub-holograms whereby error diffusion can be applied independently to each of them. The computation time can be speeded up by N/S
sub-holograms whereby error diffusion can be applied independently to each of them. The computation time can be speeded up by N/S![]() times with the use of parallel processors.
times with the use of parallel processors.
On the downside, the error in the last pixel of a segment will not be distributed to the pixel directly below it; instead it will be distributed to the one on its right. This will lead to heavier distortion at the boundaries between adjacent zones, resulting in repetitive vertical strip patterns in the reconstructed image. This problem can be reduced by applying low-pass filters (for example, using optical filtering with a 4f system) to redistribute the error signal in the phase-only hologram. The low-pass filtering diffuses the error in the last pixel of each segment to its adjacent segment.
4.7 Converting a Complex-Valued Hologram to a Binary Phase-Only Hologram with Direct Binary Search
In Section 3.3.8 it was shown that direct binary search (DBS) [15,16] can be applied to generate a binary phase-only hologram. With minor modification, the DBS can also be used to convert a complex-valued hologram into a phase-only hologram. As the source image is not available, the reconstructed image of the complex-valued hologram, denoted by H(m,n)![]() , is computed:
, is computed:
where h(m,n;z0)![]() is the free space impulse response. The image Iref(m,n)
is the free space impulse response. The image Iref(m,n)![]() is taken to be the reference image. Similar to the process in Section 3.3.8, the binary phase-only hologram is converted from the original hologram through an iterative process. Let k and Bk(m,n)
is taken to be the reference image. Similar to the process in Section 3.3.8, the binary phase-only hologram is converted from the original hologram through an iterative process. Let k and Bk(m,n)![]() denote the number of iterations that have been conducted and the corresponding binary phase-only hologram. Initially, at k= 0, pixels of Bk=0(m,n)
denote the number of iterations that have been conducted and the corresponding binary phase-only hologram. Initially, at k= 0, pixels of Bk=0(m,n)![]() are assigned random values of either 1 or 0. A reconstructed image from the binary phase-only hologram can be obtained by
are assigned random values of either 1 or 0. A reconstructed image from the binary phase-only hologram can be obtained by

where h†(m,n;z0)![]() is the conjugate of the free space impulse response. In each of the subsequent iterations, a new pixel in the binary hologram is selected along a row-by-row, left-to-right path. When each pixel is visited, its binary value is complemented. A reconstructed image IB;k(m,n)
is the conjugate of the free space impulse response. In each of the subsequent iterations, a new pixel in the binary hologram is selected along a row-by-row, left-to-right path. When each pixel is visited, its binary value is complemented. A reconstructed image IB;k(m,n)![]() of the updated binary hologram Bk(m,n)
of the updated binary hologram Bk(m,n)![]() on the focused plane is computed using Eq. (4.31). The mean square errors (MSEs) between the reference image and the reconstructed images IB;k(m,n)
on the focused plane is computed using Eq. (4.31). The mean square errors (MSEs) between the reference image and the reconstructed images IB;k(m,n)![]() and IB;k−1(m,n)
and IB;k−1(m,n)![]() are determined. If the MSE of the updated hologram is lower than that of the previous hologram at the (k − 1)th iteration, it will be retained. Otherwise, Bk(m,n)
are determined. If the MSE of the updated hologram is lower than that of the previous hologram at the (k − 1)th iteration, it will be retained. Otherwise, Bk(m,n)![]() will be replaced by Bk−1(m,n)
will be replaced by Bk−1(m,n)![]() . Subsequently, the iteration count k is increased by 1. After all the binary pixels have been evaluated, a binary phase-only hologram will be generated. The quality of the reconstructed image of the binary phase-only hologram generated with a single round of DBS is poor. This problem can be alleviated with multiple rounds of DBS.
. Subsequently, the iteration count k is increased by 1. After all the binary pixels have been evaluated, a binary phase-only hologram will be generated. The quality of the reconstructed image of the binary phase-only hologram generated with a single round of DBS is poor. This problem can be alleviated with multiple rounds of DBS.
A numerical simulation for converting a complex-valued hologram into a binary phase-only hologram with the DBS method is conducted. The source code for conducting a single epoch of DBS is shown in Section 4.8.5. When the program is executed, the user is prompted to enter an integer from 0 to 2. If the input value is 1, the binary hologram is initialized with random values and a new run of the DBS will be conducted. For an input value of 2, the DBS will be conducted based on the binary hologram generated in the previous epoch. As DBS is time consuming, the program can be stopped by the user in the middle of the process. An input value of 1 resumes the DBS after the interruption.
In the simulation, a complex-valued Fresnel hologram H(m,n)![]() of the source image “Heart” in Figure 4.11(a) is adopted. To avoid a long computation time, the sizes of the source image and its hologram are reduced to 64×64
of the source image “Heart” in Figure 4.11(a) is adopted. To avoid a long computation time, the sizes of the source image and its hologram are reduced to 64×64![]() and 128×128
and 128×128![]() , respectively. The axial distance between the hologram and the source image is 0.07 m. The reconstructed image of H(m,n)
, respectively. The axial distance between the hologram and the source image is 0.07 m. The reconstructed image of H(m,n)![]() on the focused plane, as shown in Figure 4.11(b), is computed and taken as the reference image. A binary phase-only hologram is generated after 10 rounds of DBS. The reconstructed image of the binary hologram is shown in Figure 4.11(c). The reconstructed image is similar to the reference image, with a fidelity (in PSNR) of 29.32 dB.
on the focused plane, as shown in Figure 4.11(b), is computed and taken as the reference image. A binary phase-only hologram is generated after 10 rounds of DBS. The reconstructed image of the binary hologram is shown in Figure 4.11(c). The reconstructed image is similar to the reference image, with a fidelity (in PSNR) of 29.32 dB.
Figure 4.11 (a) Source image “Heart.” (b) Reference image (reconstructed image of the complex-valued hologram). (c) Reconstructed image of binary hologram obtain with 10 rounds of DBS.
4.8 MATLAB Simulation
This section includes the MATLAB source codes employed to conduct the simulations of the methods reported in this chapter. A summary of the simulation programs (each identified by the name of its main function call) and their correspondence to previous sections are listed in Table 4.1.
Table 4.1 Summary of simulation programs in this chapter
| Function name | Description of simulation | Associated sections |
|---|---|---|
| CAM | Converting a complex-valued hologram into a phase-only hologram with the CAM method | 4.2 |
| DP | Converting a complex-valued hologram into a phase-only hologram with the double-phase macroblock method | 4.3 |
| UERD | Converting a complex-valued hologram into a phase-only hologram with the UERD method | 4.4 |
| BERD | Converting a complex-valued hologram into a phase-only hologram with the BERD method | 4.5 |
| DBS | Converting a complex-valued hologram into a binary phase-only hologram with the DBS method | 4.6 |
Three images are used to demonstrate the methods in this chapter. The first one is a planar image “Apple” that is located at an axial distance 0.08 m from the hologram. This image is used in the CAM simulation. The second image is the double-depth image “HK1” shown in Figure 1.12. The image is evenly divided into a left half-plane and a right half-plane, containing the characters H and K, respectively. The left half-plane is located at a distance of 0.07 m from the hologram plane, while the right half-plane is placed farther away at 0.08 m. This image is adopted in the simulation of the double-phase, UERD, and BERD methods. A smaller image, “Heart,” is used in the simulation of the DBS method.
4.8.1 Simulation of Converting a Complex-Valued Hologram into a Phase-Only Hologram with the CAM Method
The source code for this simulation is shown in Table 4.2. A complex-valued digital Fresnel hologram of a planar image is generated. The hologram is then converted into a phase-only hologram with the CAM method. To begin with, the main function “CAM” is called to load the source image file. Next, the function “Holo_gen” is applied to convert the source image into a complex-valued Fresnel hologram. The user is prompted to input a value for the parameter β. Based on Eqs. (4.2) and (4.5), the complex-valued hologram is converted into a phase-only hologram with the function “CAM_GEN.” Subsequently, the reconstructed image at the focused plane is computed from the phase-only hologram with the function “Holo_recon.” The reconstructed image is then displayed and saved. The function “PSNR” is called to determine the fidelity, in PSNR, of the reconstructed image as compared with the source image.
4.8.2 Simulation of Converting a Complex-Valued Hologram into a Phase-Only Hologram with the Double-Phase Macroblock Method
In this simulation, a complex-valued digital Fresnel hologram of a planar image is generated. The source code is shown in Table 4.3. The hologram is then converted into a phase-only hologram with the double-phase macroblock method. To begin with, the main function “DP,” is called to load the source image file. Next, the function “Holo_gen” is applied to convert the source image into a complex-valued Fresnel hologram. The user will be prompted to select either the 1×2![]() or the 2×2
or the 2×2![]() macro-pixel topology, and the complex-valued hologram will be converted into a phase-only hologram with the function “Interleave.” Subsequently, the reconstructed image at the focused plane will be computed from the phase-only hologram with the function “Holo_recon.” The reconstructed image is then displayed and saved in a file.
macro-pixel topology, and the complex-valued hologram will be converted into a phase-only hologram with the function “Interleave.” Subsequently, the reconstructed image at the focused plane will be computed from the phase-only hologram with the function “Holo_recon.” The reconstructed image is then displayed and saved in a file.
Table 4.3 Simulation of generating a phase-only hologram with the double-phase macroblock method
4.8.3 Simulation of Converting a Complex-Valued Hologram into a Phase-Only Hologram with the UERD Method
The source code of this simulation is shown in Table 4.4. The main function “UERD” is executed to load the double-depth image “HK1,” from which a complex-valued Fresnel hologram is generated with the function “Holo_gen.” Next, the function “UERD_convert” is applied to convert the complex-valued hologram into a phase-only hologram. In this process, hologram pixels are scanned from the first row to the last row, and in each row in a left-to-right direction. The magnitude of each visited pixel is set to unity, and the error is distributed to its four neighbors. Upon completion of the scanning process, a phase-only hologram is obtained. Subsequently, the reconstructed images of the phase-only hologram on two focused planes are computed with the function “Holo_recon.” The reconstructed images is then displayed and saved.
Table 4.4 Converting a complex-valued hologram into a phase-only hologram with the UERD method
4.8.4 Simulation of Converting a Complex-Valued Hologram into a Phase-Only Hologram with the BERD Method
In this simulation, a digital phase-only Fresnel hologram of a double-depth image is generated. The source code is shown in Table 4.5. To begin, in the main function “BERD” the double-depth image “HK1” is loaded, from which a complex-valued hologram is generated with the function “Holo_gen.” Next, the function “BERD_convert” is applied to convert the complex-valued hologram into a phase-only hologram. The process is similar to the UERD method described in Section 4.8.3, with the exception that the direction of scanning for the even and the odd rows is reversed. Subsequently, the reconstructed image at the focused plane will be computed from the phase-only hologram with the function “Holo_recon.” The reconstructed image is then displayed and saved.
4.8.5 Simulation of Converting a Complex-Valued Hologram into a Binary Phase-Only Hologram with the DBS Method
In this simulation, a digital phase-only Fresnel hologram of a planar image is generated. The source code is shown in Table 4.6. In the main function “DBS,” the image “Heart” is loaded, from which a complex-valued hologram is generated with the function “Holo_gen.” Next, the user is prompted to enter a value of 0, 1, or 2. The input value indicates whether the DBS should be conducted as a new run (0), resume from the previous run (1), or as a new epoch based on the binary hologram obtained in the previous run (2). Upon completion of a complete round of DBS, or when the process is stopped by the user, the reconstructed image at the focused plane is computed from the phase-only hologram with the function “Holo_recon.” The reconstructed image is then displayed and saved.
4.9 Summary
In Chapter 3 a number of methods were described for generating a phase-only hologram of an object. However, these methods are not applicable if the source image of the object is not present and only its hologram is available. Such a situation happens if a hologram is directly captured from a physical object (for example, applying phase-shifting holography) instead of generated from a numerical graphic model. This chapter describes six methods for converting a complex-valued hologram into a phase-only hologram. The first two methods, CAM and double-phase methods, convert a complex-valued hologram into a pure phase representation. When the latter is displayed on an SLM with suitable optical filtering, a visual 3-D image is reconstructed. The third to fifth methods apply different variants of the Floyd–Steinberg error diffusion algorithm to convert a complex-valued hologram into a continuous tone phase-only hologram. Among these three error diffusion methods, BERD results in the best reconstructed image, while the LERD method can be implemented with parallel computing devices such as GPUs. The last method, DBS, converts a complex-valued hologram into a binary phase-only hologram through an iterative process. Compared with other methods, the quality of the reconstructed image is generally poor unless more iterations are performed at the expense of longer computation time. A phase-only hologram generated by error diffusion or DBS can be displayed directly with a phase-only SLM without additional optical processing.
Table 4.6 Converting a complex-valued hologram into a binary phase-only hologram with the DBS method
Exercises
E.4.1 A hologram is converted into a phase-only hologram and reconstructed with the CAM method. Based on the MATLAB code in Section 4.8.1, write a program to compute the difference (in PSNR) between the reconstructed image of the original hologram and the one obtained with the CAM method, as a function of β
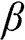 .
.
E.4.2 Further to E.4.1, plot the PSNR versus β
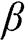 , and determine the optimal value of β
, and determine the optimal value of β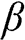 that results in the maximum PSNR value?
that results in the maximum PSNR value?
E.4.3 Referring to Eq. (4.6), determine the double-phase representation of the complex number (0.5+i0.3)
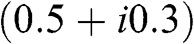 .
.
E.4.4 In Eq. (4.7), a binary double-phase hologram can be implemented by quantizing the phase components θ1(x,y)
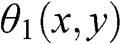 and θ2(x,y)
and θ2(x,y)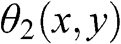 into a bi-level representation. Based on the MATLAB code in Section 4.8.2, generate a binary double-phase hologram with the 2 × 2 macro-pixel topology. Evaluate the visual quality and the PSNR of the reconstructed image of the binary double-phase hologram compared with the one obtained with the original complex-valued hologram.
into a bi-level representation. Based on the MATLAB code in Section 4.8.2, generate a binary double-phase hologram with the 2 × 2 macro-pixel topology. Evaluate the visual quality and the PSNR of the reconstructed image of the binary double-phase hologram compared with the one obtained with the original complex-valued hologram.
E.4.5 Repeat E.4.4 with a binary double-phase hologram that generated with the 1 × 2 macro-pixel topology.
E.4.6 A pixel in a complex-valued hologram has a value of (1.2+i2.0)
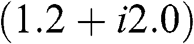 . Determine the error resulting from setting the magnitude of the pixel value to unity. The error is distributed to the four neighboring pixels with the Floyd–Steinberg error diffusion algorithm. What will be the error imparted to each pixel?
. Determine the error resulting from setting the magnitude of the pixel value to unity. The error is distributed to the four neighboring pixels with the Floyd–Steinberg error diffusion algorithm. What will be the error imparted to each pixel?










