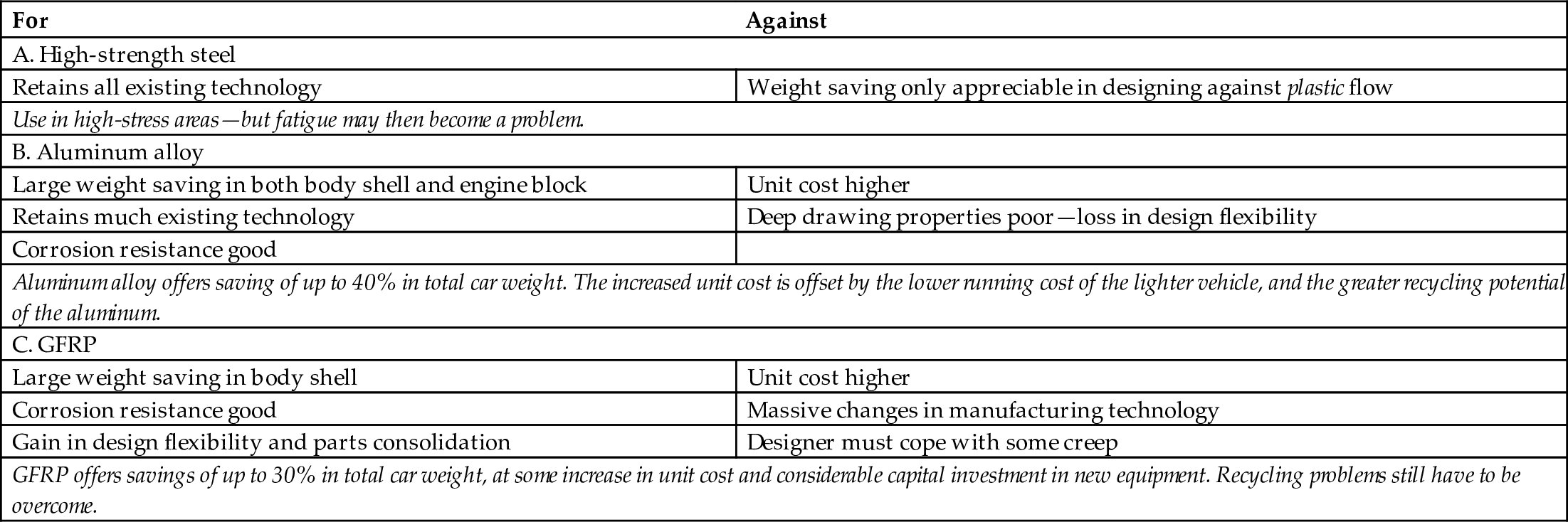
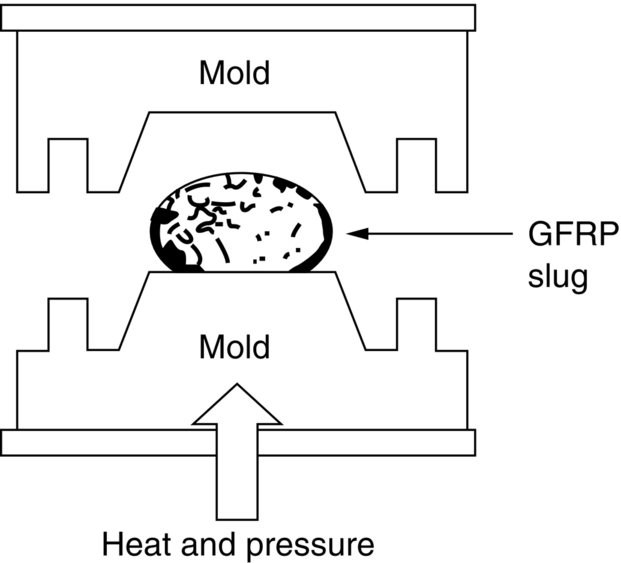
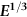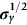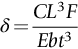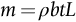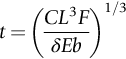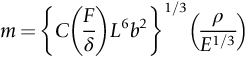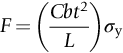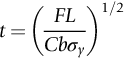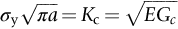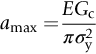section epub:type=”chapter”> The status of steel as the raw material of choice for the manufacture of car bodies rests principally on its price. It has always been the cheapest material that meets the necessary strength, stiffness, formability, and weldability requirements of large-scale car body production. Until recently, the fact that steel has a density two-thirds that of lead accorded little significance. But increasing sustainability awareness and legislative requirements concerning carbon emissions are now changing that view. Car makers are looking hard at alternative materials. Energy is used to build a car and energy is used to run it. High oil prices mean that the cost of the gas consumed during the life of a car is comparable with the cost of the car itself. Consumers now want more fuel-efficient cars, and more fuel-efficient cars have lower carbon emissions. This chapter addresses these concerns. The chapter discusses various ways of achieving energy economy. The chapter also focuses on alternative materials that can be used, which is divided into primary mechanical properties and secondary properties. Although resistance to deflection and plastic yielding are obviously of first importance in choosing alternative materials, other properties too enter into the selection. The chapter concludes with a discussion of various production methods of cars. The status of steel as the raw material of choice for the manufacture of car bodies rests principally on its price. It has always been the cheapest material that meets the necessary strength, stiffness, formability, and weldability requirements of large-scale car body production. Until recently, the fact that steel has a density two-thirds that of lead was accorded little significance. But increasing sustainability awareness and legislative requirements concerning carbon emissions are now changing that view. Car makers are looking hard at alternative materials. Energy is used to build a car, and energy is used to run it. Oil prices mean that the cost of the gas consumed during the life of a car is comparable with the cost of the car itself. Consumers want more fuel-efficient cars, and more fuel-efficient cars have lower carbon emissions. This trend is magnified by the taxation policies of governments. Fuel duties have increased, so one way in which the motorist can offset the effects of additional fuel taxation is to reduce fuel consumption per mile. However, this strategy can be partly countered by imposing annual taxes on vehicles that relate to their carbon emissions. This acts as a driver to reduce engine power—effectively vehicle size. The extent to which governments really care about sustainability and carbon emissions—or are using these as a front for generating yet further taxation revenues—is open to question. But the way in which the economics are felt at consumer level is the same, and likely to get much worse in the longer term. It is clear from Table 33.1 that the energy content of the car itself—the steel, rubber, glass, and manufacturing process—is small: less than 10% that required to move the car. This means there is little point trying to save energy here; indeed (as we shall see) it may pay to use more energy to make the car (using, for instance, aluminum instead of steel) if this reduces fuel consumption. Table 33.1 We must focus, then, on reducing the energy used to move the car. The following are the two routes. We can reduce the size of cars, but the consumer does not like that. Or we can reduce the weight of the car by substituting lighter materials for those used now. Lighter cars not only use less fuel, but they also have lower carbon emissions—hence, the interest in producing lighter vehicles, reversing a consistent trend in the opposite direction. As Figure 33.1 suggests, most cars weigh between 400 kg and 2500 kg. In a typical modern production car (Figure 33.2), this is made up as shown in Table 33.2. Table 33.2 Candidate materials for substitutes must be lighter than steel, but structurally equivalent. For the engine block, the choice is obvious: aluminum (density 2.7 Mg m–3) or possibly magnesium (density 1.8 Mg m–3) replace an equal volume of cast iron (density 7.7 Mg m–3) with an immediate weight reduction on this component of 2.8 to 4.3 times. The production methods remain almost unchanged. Most manufacturers have made this change; cars like the one shown in Figure 33.3 are a thing of the past. The biggest potential weight saving, however, is in the body panels, which make up 60% of the weight of the vehicle. Here the choice is more difficult. Candidate materials are given in Table 33.3. How do we assess the possible weight saving? Just replacing a steel panel with an aluminum-alloy or fiberglass one of equal thickness (giving a weight saving that scales as the density) is unrealistic: both substitutes have much lower moduli, and thus will deflect (under given loads) far more; and one of them has a much lower yield strength, and might undergo plastic flow. If (as with body panels) elastic deflection is what counts, the logical comparison is for a panel of equal stiffness. And if resistance to plastic flow counts (as with fenders) then the proper thing to do is compare sections with equal resistance to plastic flow. The elastic deflection δ of a panel under a force F (Figure 33.4) is given by where t is the sheet thickness, L the length, and b the width of the panel. The constant C depends on how the panel is held: at two edges, at four edges, and so on—it does not affect our choice. The mass of the panel is The quantities b and L are determined by the design (they are the dimensions of the door, trunk lid, etc.). The only variable in controlling the stiffness is t. Now from Equation (33.1) Substituting this expression for t in Equation (33.2) gives the mass of the panel shown in Equation (33.4). For a given stiffness (F/δ), panel dimensions (L, b), and edge-constraints (C), the lightest panel is the one with the smallest value of ρ/E1/3. We can do a similar analysis for plastic yielding. A panel with the section shown in Figure 33.5 yields at a load The panel mass is given by Equation (33.2). The only variable is t, from Equation (33.5). Substituting for t in Equation (33.2) gives The panel with the smallest value of We can now assess candidate materials more sensibly on the basis of the data given in Table 33.3. The values of the property groups are shown in the last two columns. For most body panels (elastic deflection determines design) high-strength steel offers no advantage over mild steel: it has the same value of ρ/E1/3. GFRP is better (a lower ρ/E1/3 and weight), and aluminum alloy is better still—that is one of the reasons aircraft are made of aluminum. But the weight saving in going from steel to aluminum is not a factor of 3 (the ratio of the densities) but only 2 (the ratio of ρ/E1/3) because the aluminum panel has to be thicker to compensate for its lower E. High-strength steel does offer a weight saving for strength-limited components: fenders, front and rear header panels, engine mounts, bulkheads, and so forth—the weight saving Although resistance to deflection and plastic yielding are obviously of first importance in choosing alternative materials, other properties enter into the selection. Table 33.4 lists the conditions imposed by the service environment. Elastic and plastic deflection we have dealt with already. The toughness of steel is so high that fracture of a steel panel is seldom a problem. But what about the other materials? The data for toughness are given in Table 33.5. But what is the proper way to use toughness values? Suppose the panel is loaded up to its yield load (above this load we know it will begin to fail by plastic flow so it does not matter whether other failure mechanisms also appear)—what is the maximum crack size that is still stable? If this is large enough that it should not appear in service, we are satisfied; if not, we must increase the section. This crack size is given conservatively by from which The resulting crack lengths are given in Table 33.5. A panel with a longer crack will fail by “tearing”; one with a short crack will fail by general yield—it will bend permanently. Although the crack lengths are shorter in replacement materials than in steel, they are still large enough to permit the replacement materials to be used. Fatigue (Chapter 18) is always a potential problem with any structure subject to varying loads: anything from the loading due to closing the door to that caused by engine vibration can, potentially, lead to failure. The fatigue strength of all these materials is adequate. Creep (Chapter 21) is not normally a problem a designer considers when designing a car body with metals: the maximum service temperature reached is 60°C, and neither steel nor aluminum alloys creep significantly at these temperatures. But GFRP does, so extra reinforcement or heavier sections may be necessary where temperatures exceed this value. More important than creep or fatigue in current car design is the effect of environment. A significant part of the cost of a car is contributed by the manufacturing processes designed to prevent rusting; and these processes only partly work—it is body rust that ultimately kills a car, since the mechanical parts (brake discs, etc.) can be replaced relatively easily. Steel is particularly bad in this regard. Under ordinary circumstances, aluminum is much better. Although the effect of salt on aluminum is bad, heavy anodizing will slow down even that form of attack to tolerable levels (yacht masts are made of anodized aluminum alloy). So aluminum alloy is good: it resists all the fluids likely to come in contact with it. What about GFRP? The strength of GFRP is reduced by up to 20% by continuous immersion in most of the fluids—even salt-water—with which it is likely to come into contact; but (as we know from fiberglass boats) this drop in strength is not critical, and it occurs without visible corrosion, or loss of section. In fact, GFRP is much more corrosion-resistant, in the normal sense of “loss-of-section,” than steel The biggest penalty one has to pay in switching materials is likely to be the higher material and production costs. High-strength steel, of course, presents almost no problem. The yield strength is higher, but the section is thinner, so that only slight changes in punches, dies, and presses are necessary, and once these are paid for, the extra cost is just that of the material. At first sight, the same is true of aluminum alloys. But because they are heavily alloyed (to give a high yield strength) their ductility is low. If expense is unimportant, this does not matter; some early Rolls-Royce cars (Figure 33.6) had aluminum bodies which were formed into intricate shapes by laborious hand-beating methods, with frequent annealing of the aluminum to restore its ductility. But in mass production we should like to deep draw body panels in one operation—and then low ductility is much more serious. The result is a loss of design flexibility: there are more constraints on the use of aluminum alloys than on steel; and it is this, rather than the cost, that is the greatest obstacle to the wholesale use of aluminum in cars. GFRP looks as if it would present production problems: you may be familiar with the tedious hand layup process required to make a fiberglass boat or canoe. But mass-production methods have now been developed to handle GFRP. Most modern cars have GFRP components (fenders, facia panels, internal panels) and a few have GFRP bodies (Figure 33.7), usually mounted on a steel chassis; the full weight savings will only be realized if the whole load-bearing structure is made from GFRP. In producing GFRP car panels, a slug of polyester resin, with chopped glass fibers mixed in with it, is dropped into a heated split mold (Figure 33.8). As the polyester used is a thermoset it will “go off” in the hot mold, after which the solid molding can be ejected. Modern methods allow a press like this to produce one molding per minute—still slower than steel pressing, but practical. Molding brings certain advantages. It offers design flexibility—particularly in change of section, and sharp detail—which are not easily achieved with steel. And GFRP moldings often result in consolidation of components, reducing assembly costs.
Final Case Study: Materials and Energy in Car Design
Publisher Summary
33.1 Introduction
33.2 Energy and Carbon Emissions
33.3 Achieving Energy Economy
Energy to produce cars, per year
=
0.8% to 1.5% of total energy consumed by nation
Energy to move cars, per year
=
15% of total energy consumed by nation
Transportation of people and goods, total
=
24% of total energy consumed by nation
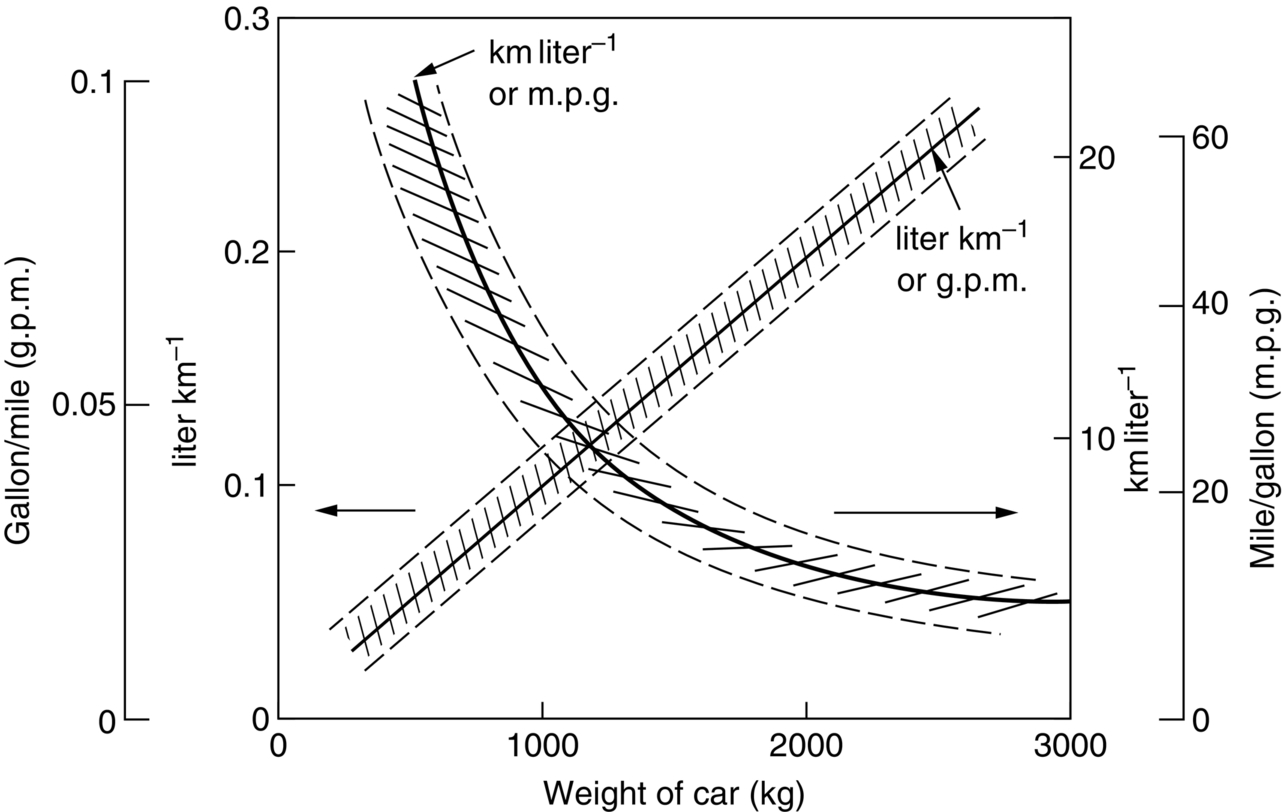
33.4 Material Content of a Car
Material
Component
71% steel
Body shell; panels
15% cast iron
Engine block; gear box; rear axle
4% rubber
Tires; hoses
Balance
Glass, zinc, copper, aluminum, polymers
33.5 Alternative Materials
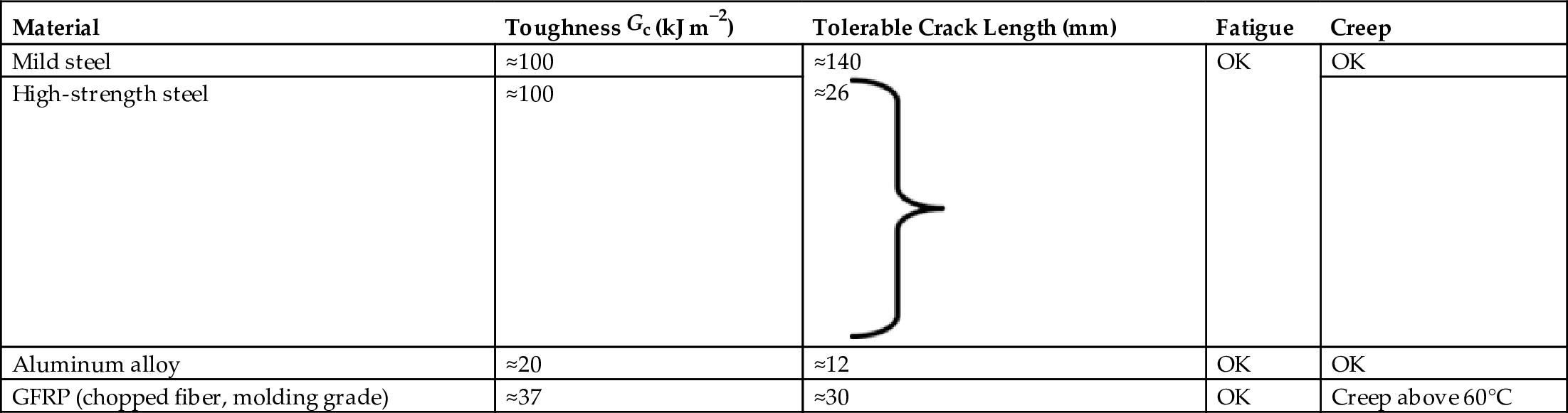
Primary mechanical properties
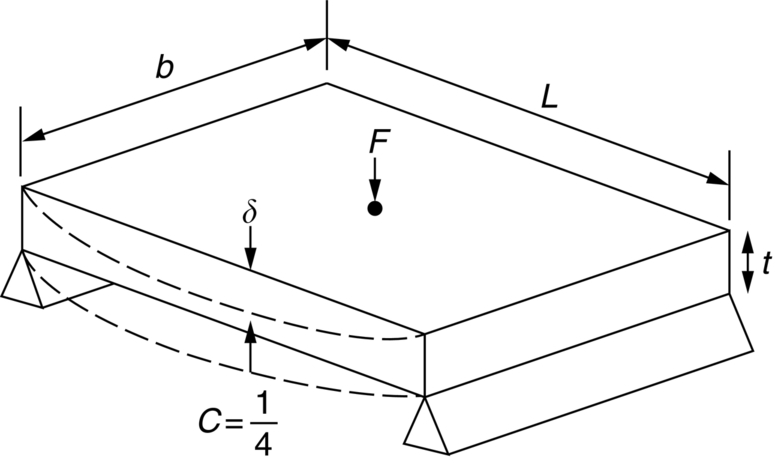
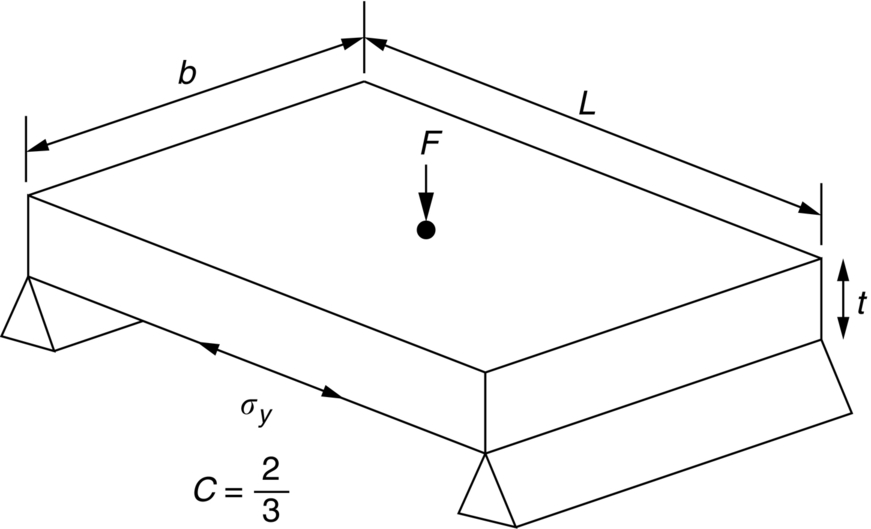
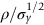is the one we want.
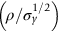is a factor of 1.5. Both aluminum alloy and fiberglass offer potential weight savings of up to 3 times 
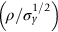on these components. This makes possible a saving of at least 30% on the weight of the vehicle—if an aluminum engine block is used, the overall weight saving is larger still. These are very substantial savings—sufficient to achieve a 50% increase in mileage per gallon without any decrease in size of car or increase in engine efficiency. So they are obviously worth examining more closely. What, then, of the other properties required of the substitute materials?
Secondary properties
33.6 Production Methods
33.7 Conclusions
