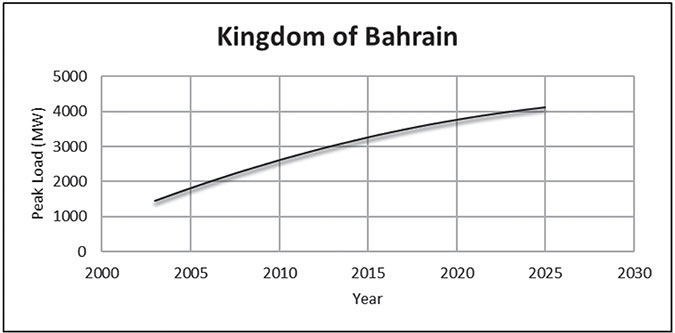
Accurate models for electric power load forecasting (EPLF) are essential to the operation and planning of a utility company. The load forecasting helps an electric utility to make important decisions, including decisions on purchasing and generating electric power, load switching, and infrastructure development. Load forecasts are extremely important for energy suppliers, financial institutions, and other participants in electric energy generation, transmission, distribution, and markets (He and Zheng, 2018; Jung et al., 2018).

Load forecasts can be divided into three categories (Hsu and Chen, 2003; Papadakis et al., 2003; Al-Kandari et al., 2004):

The forecasts for different time horizons are important for different operations within a utility company. The natures of these forecasts are different as well. For example, for a particular region, it is possible to predict the next day load with an accuracy of approximately 1–3%. However, it is impossible to predict the next year’s peak load with a similar accuracy since accurate long-term weather forecasts are not available. For the next year’s peak forecast, it is possible to provide the probability distribution of the load based on historical load data. It is also possible, according to the industry practice and economic growth to predict the next year’s peak load.

Load forecasting has always been important for planning and operational decision conducted by utility companies. However, with the deregulation of the energy industries, load forecasting is even more important.

In the deregulated economy, decisions on capital expenditures based on long-term forecasting are also more important than in a non-deregulated economy when rate increases could be justified by capital expenditure projects.

Load forecasting methodologies developed may be classified into two broad categories: autonomous models and conditional models. Autonomous models attempt to relate future growth of electricity demand on a system based on its past growth, and conditional models attempt to relate it to other variables, mainly economic indicators.

The load in GCC countries follows almost the same pattern, which is the peak load during the summer season. It is almost doubled the peak in the winter season. So the annual load has been divided into two categories, winter season (low season) and summer season (high season). As stated by Sayed M. Salem (Islam et al., 1995), this will minimize the error and gave a better prediction. After categorizing the load, the percentage increase between 2004 and 2005 for both categories has been calculated. Each category of the year 2005 is multiplied by its relevant percentage, and the same procedure done for the years until 2015. Each load calculated by this technique is added to the historical data and feed to the neuro-fuzzy system to predict the next year.

In recent years, the artificial neural networks (ANN) and fuzzy logic (FL) systems have each providing very encouraging results in solving the problems. This has encouraging researchers to combine both ANN and FL in an attempt to create a final system that reduces the limitations of each of these individual techniques (Tamimi and Egbert, 2000). The strength of this technique lies in its ability to reduce appreciable computational time and its comparable accuracy with other modeling techniques (Metaxiotis et al., 2003) and (Padmakumari et al., 1999). The definition of a neuro-fuzzy system is a combination of ANN and fuzzy inference system (FIS) in such a way that neural network learning algorithms are used to determine the parameters of FIS (Al-Kandai et al., 2003; Mielczarski, 1995). An even more important aspect is that the system should always be interpretable in terms of fuzzy if-then rules, because it is based on the fuzzy system reflecting vague knowledge.

Neural Networks and FL are both complementary technologies in the design of intelligent systems. Each method has merits and demerits. Neural networks are essentially low-level computational structures and algorithms that offer good performance in dealing with sensory data. On the other hand, the FL techniques often deal with issues, such as reasoning, on a higher level than neural networks. However, since fuzzy systems do not have much learning capability, it is difficult for a human operator to tune the fuzzy rules and membership functions from the training data set. Also, because the internal layers of neural networks are always opaque to the user, the mapping rules in the network are not visible and are difficult to understand. Furthermore, the convergence of learning is usually very slow and not guaranteed. Thus, a promising approach for getting the benefits of both fuzzy systems and neural networks is to merge them into an integrated system. This collaboration will possess the advantages of both neural networks (e.g., learning and optimization abilities) and fuzzy systems (e.g., human-like IF-THEN rules thinking and ease of incorporating expert knowledge).

Fuzzy reasoning usually performed using if-then rules. The fuzzy rules define the connection between input and output fuzzy (linguistic) variables. The rules consist of two parts:

$\begin{array}{c}\underset{\text{A Consequence part}}{\underbrace{IF\text{ Month is July and Temperature is High}}}\underset{\text{An Antecedent part}}{\underbrace{THEN\text{ Load is High}}}\end{array}$

For more details, it can be referred in Mielczarski (1995). In the above fuzzy rules, month, temperature level and load are called fuzzy variable and July, high, and high as a linguistic variable. AND is a connective operation, OR is a union and NOT is a complement. It aggregates the results with the premise part.

From a given input to output, using fuzzy logic, Fuzzy Inference (FI) is the actual process of mapping. A number of names know the FIS. These names are:

Any FIS has to be defined. This FIS is needed to define the Fuzzy Knowledge Base. The Fuzzy Knowledge Base defined as a rule base having a number of fuzzy and a database that defines the membership functions of fuzzy sets.

There are a number of statements (three) coming out of the Fuzzy Knowledge Base. These three statements are Fuzzifier, Inference Engine, and Defuzzifier. The Fuzzifier is the crisp inputs are exact inputs measured by sensors and passed into the control system for processing. The Inference Engine can be defined as the engine between the Fuzzifier and Defuzzifier. The Defuzzifier of the Output Variable that represents the converging of the fuzzy output of the inference engine to a crisp using membership functions analogous to the ones used by the Fuzzifier.

The Electrical long-term peak load demand forecasting using a developed adaptive neuro-fuzzy inference system (ANFIS). It is important to develop a suitable model, which can be used in different types of softwares to calculate electric load forecasting and different output requested by decision-makers. The developed models should have an acceptable level of mean errors. Having a simple and pragmatic equation can provide an acceptable model to make plans for periodical operations, energy trading, and facility expansion in the electricity sector. The estimated peak load models help energy policymakers in different countries. This means that it will encourage in the development of the countries through the energy field and setting the future plan for the countries. It also helps with finding a suitable instant for electrical energy trading.

For the electricity sector decision-makers, energy trading and facility expansion are required. The electricity demand pattern is multifaceted due to the different types of loads and weather conditions. Therefore, finding an appropriate peak load-forecasting model for the country’s peak demand of the electricity network is an important task for network planning and power trading. This will help in the planning of a reliable and economical operated network.

There are many exogenous variables for the long-term load forecasting (LTLF)-like weather conditions, industrial development, Population Growth, and social events in the country. For more simplicity, the model uses the main variables, which affect the peak load demand and selected for the proposed Model.

ANFIS Models are designed for output estimated Long Term Estimated Load for a number of countries. The FIS performs fuzzy reasoning. It was designed for output estimated Long Term Estimated Load for the countries if planned to estimate the peak load for the future. The MATLAB Simulink 7.10 package is suitable and well to be used to obtain the estimated peak load for the countries.

Neuro-fuzzy systems allow the incorporation of both numerical and linguistic data into the system. The neuro-fuzzy system is also capable of extracting fuzzy knowledge from numerical data. The neuro-fuzzy systems divided into two main groups, the neural FISs, and fuzzy neural networks. Various neural networks, e.g., Multilayer Perceptions (MLP) or Radial-Basis Function Networks are capable of learning nonlinear mappings and generalizing over a set of methods very accurately. Rule-based neural networks implement a FL system.

EPLF is an essential process in the planning of electrical utilities and the operation of the power systems for the utilities. Perfect estimation for load forecasting is the way towards economic saving in operating and maintenance costs. Many studies were done a long time ago and present, where a model of the peak load for the Kingdom of Bahrain to forecast the peak load demand for the upcoming years using polynomial is presented in the present chapter. This type of study helps with increasing the reliability of power supply and delivery system, and making the correct decisions for future development.

Electric peak load demand is the highest recorded demand and is supplied by generators. It is recorded for different time horizons. The estimated and recorded peal load can be on hourly, daily, weekly, monthly, or yearly basis. The EPLF has different characteristics compared to other types of energy commodities. This type of energy should be consumed as soon as it was generated. Electricity Load Forecasting for the peak load that made for various purposes can be classified into three categories. These three categories are short-term, medium-term, and long-term forecasts.

The developing countries like the GCC countries have a peak load growth in electricity mainly based on variables such as economic growth, population, and efficiency standards, coupled with other factors inherent in the mathematical development of forecasting models making accurate projections difficult. The practical outage data statistics collection is helping in the development of methods and models. The study is helping in identifying design variables to reduce the level of risk.

The studies are serving to establish the LTLF, which is used to estimate the load for more than one year, where it is usually used for a period of 20 years, or more years in some cases. The target of this type of forecasting is to plan for the install capacity that helping to build it in the future for the expected load demand based on the projects and the master plan of the country. For example, the LTLF helps the country in allocating and involving the independent power companies to participate in bidding for building power generation or to plan purchasing electrical energy for a long period to manage the energy demand in a most economical and reliable way.

The medium-term load forecast (MTLF) can be used to predict the load from one week to one year. The target of this type of forecasting is to enable electricity utilities and trading companies to estimate the load demand for less than one year and greater than short term load forecast (STLF) period. The MTLF helps the electricity sector companies to negotiate contracts with other companies and to schedule the operations and maintenance.

The STLF is the target to predict the load up to one week. It is used for daily power system operation. The very short-term load forecast (VSTLF) is used for less than one day forecast to meet the load demand during the day in the energy market.

Other important points regarding the estimated electric load study are to avoid the huge in generation capacity in the mid-term and long-term plans, which help the countries to avoid the load shedding and to meet the energy demand in different sector(s). These will help the economic development of the countries.