15.1 Introduction

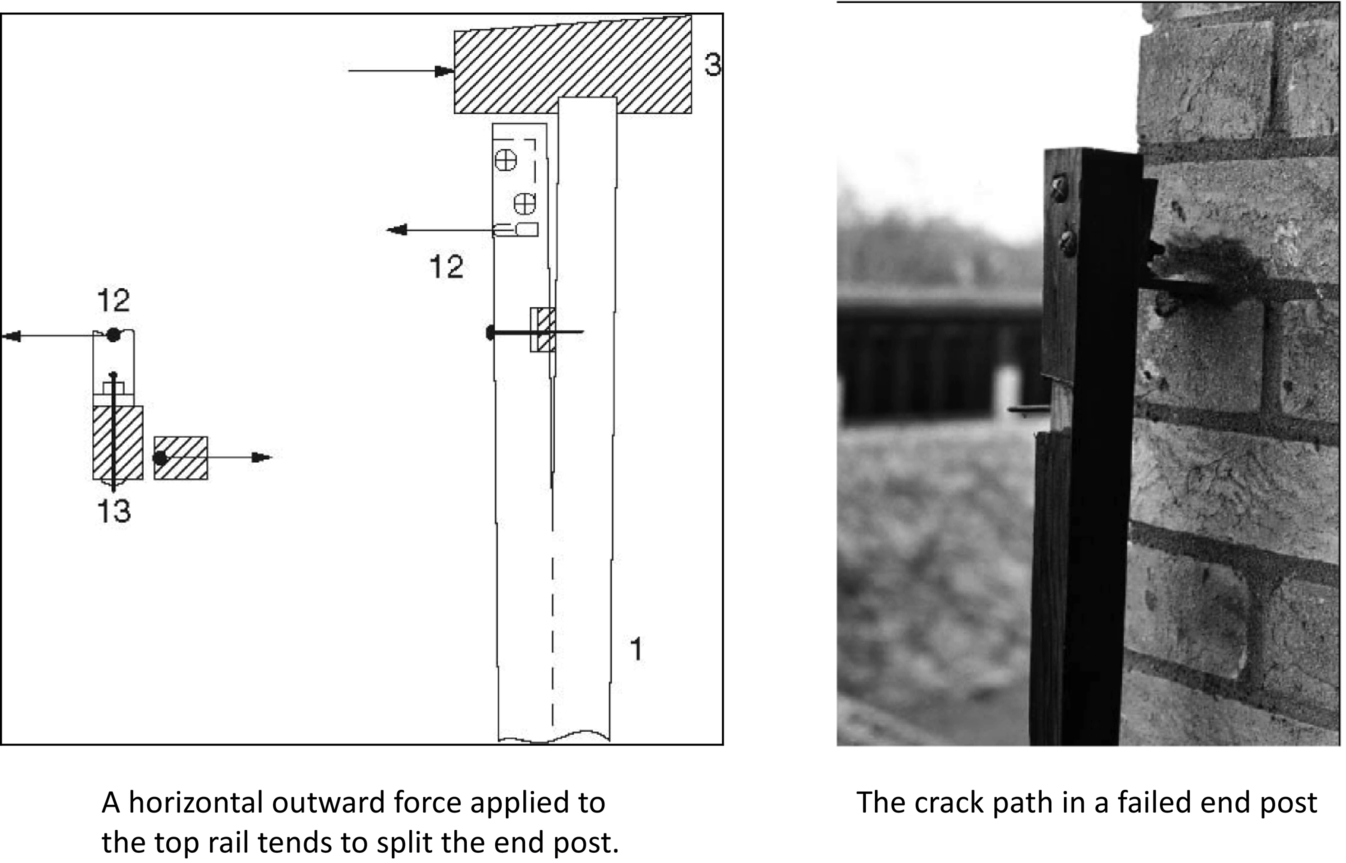
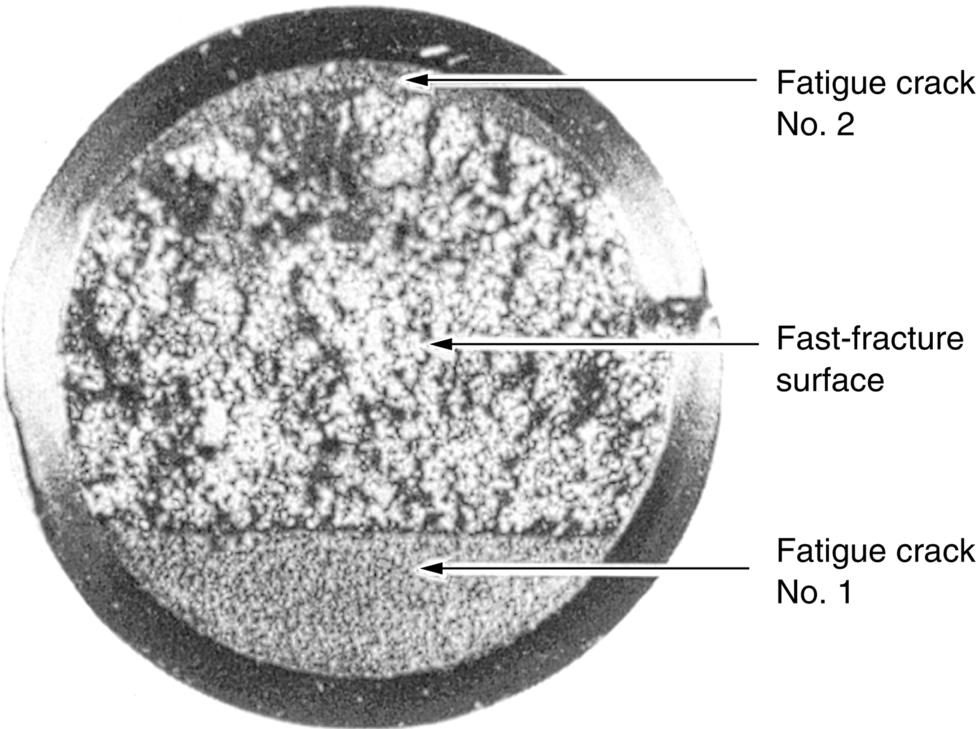
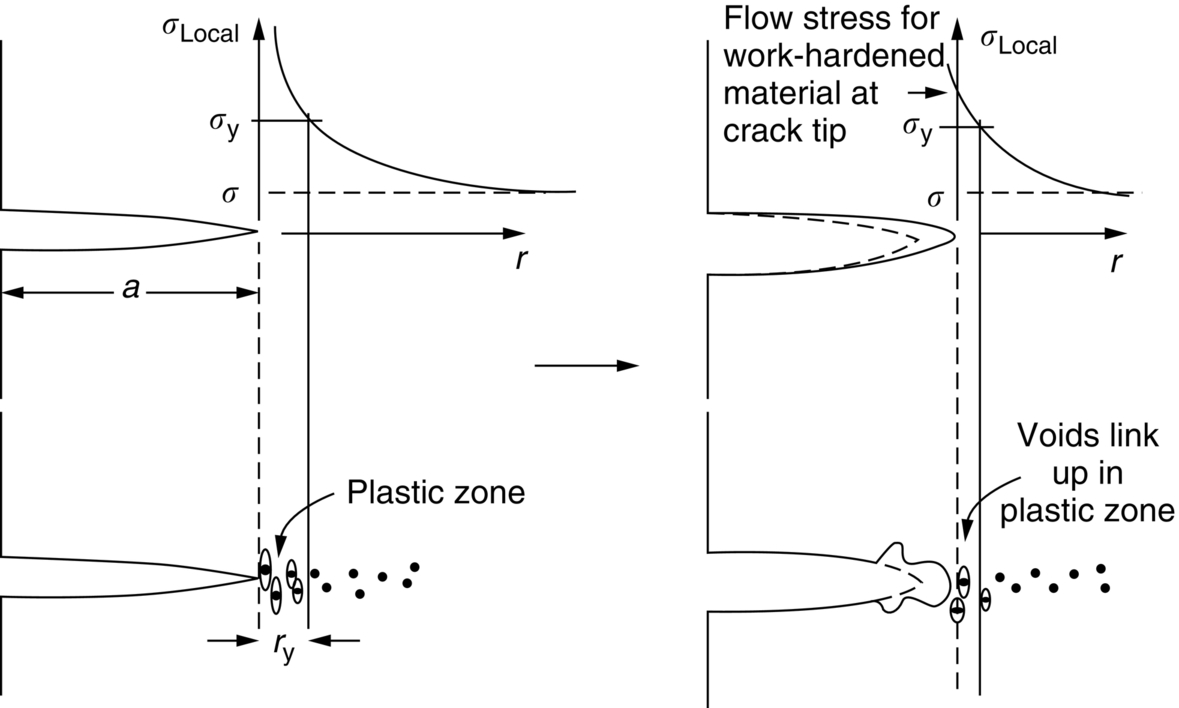
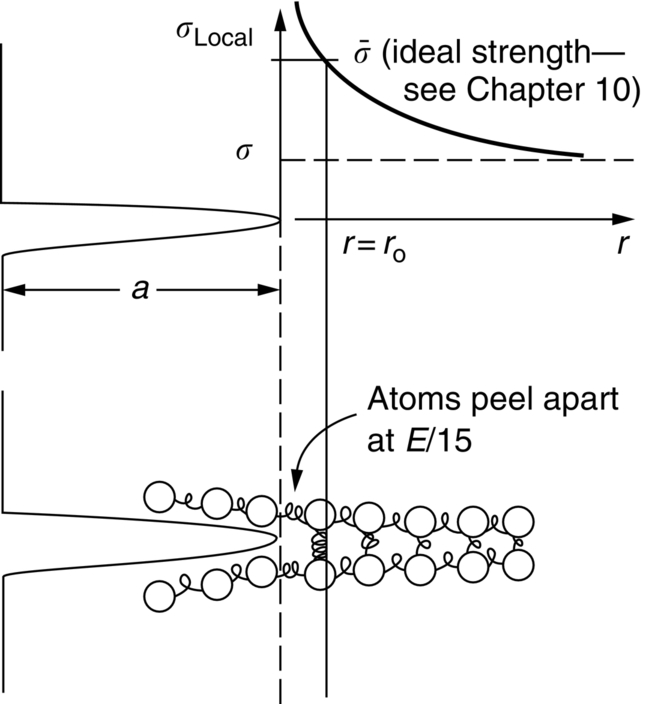
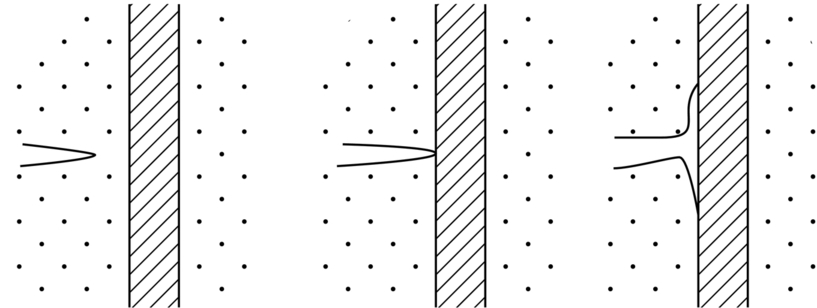
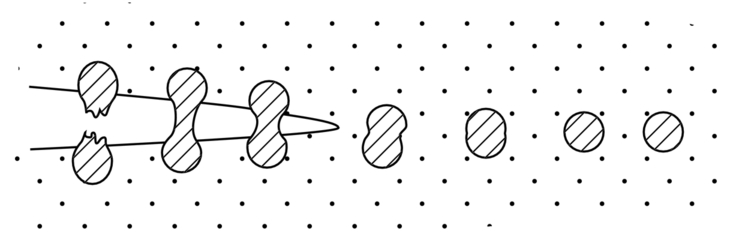
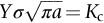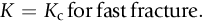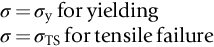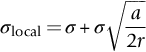In Chapter 14 we showed that, if a material contains a crack and is sufficiently stressed, the crack becomes unstable and grows—at up to the speed of sound in the material—to cause catastrophically rapid fracture, or fast fracture at a stress less than the yield stress. We were able to quantify this phenomenon and obtained a relationship for the onset of fast fracture

Yσπa=Kc

15.2 Mechanisms of Crack Propagation 1: Ductile Tearing

Let us first of all look at what happens when we load a cracked piece of a ductile metal—in other words, a metal that can flow readily to give large plastic deformations (e.g., pure copper; or mild steel at, or above, room temperature). If we load the material sufficiently, we can get fracture to take place starting from the crack. If you examine the surfaces of the metal after it has fractured (Figure 15.1) you see that the fracture surface is extremely rough, indicating that a great deal of plastic work has taken place.

Let us explain this observation. Whenever a crack is present in a material, the stress close to the crack, σ_local, is greater than the average stress σ applied to the piece of material; the crack has the effect of concentrating the stress. Mathematical analysis shows that the local stress ahead of a sharp crack in an elastic material is

σlocal=σ+σa2r

The closer one approaches to the tip of the crack, the higher the local stress becomes, until at some distance r_y from the tip of the crack the stress reaches the yield stress, σ_y of the material, and plastic flow occurs (Figure 15.2). The distance r_y is easily calculated by setting σ_local = σ_y in Equation (15.1). Assuming r_y to be small compared to the crack length, a, the result is

ry=σ2a2σy2=K22πσy2

The crack propagates when K is equal to K_c; the width of the plastic zone, r_y, is then given by Equation (15.2) with K replaced by K_c. Note that the zone of plasticity shrinks rapidly as σ_y increases: cracks in soft metals have a large plastic zone; cracks in hard ceramics have a small zone, or none at all.

Even when nominally pure, most metals contain tiny inclusions (or particles) of chemical compounds formed by reaction between the metal and impurity atoms. Within the plastic zone, plastic flow takes place around these inclusions, leading to elongated cavities, as shown in Figure 15.2. As plastic flow progresses, these cavities link up, and the crack advances by means of this ductile tearing. The plastic flow at the crack tip naturally turns our initially sharp crack into a blunt crack, and it turns out from the stress mathematics that this crack blunting decreases σ_local so that, at the crack tip itself, σ_local is just sufficient to keep on plastically deforming the work-hardened material there, as the figure shows.

The important thing about crack growth by ductile tearing is that it consumes a lot of energy by plastic flow; the bigger the plastic zone, the more energy is absorbed. High energy absorption means that G_c is high, and so is K_c. This is why ductile metals are so tough. Other materials, too, owe their toughness to this behavior—plasticine is one, and some polymers also exhibit toughening by processes similar to ductile tearing.

15.3 Mechanisms of Crack Propagation 2: Cleavage

As we showed in Chapter 9, ceramics and glasses have very high yield strengths, and thus very little plastic deformation takes place at crack tips in these materials. Even allowing for a small degree of crack blunting, the local stress at the crack tip is still in excess of the ideal strength and is thus large enough to literally break apart the interatomic bonds there; the crack then spreads between a pair of atomic planes giving rise to an atomically flat surface by cleavage (Figure 15.3). The energy required simply to break the interatomic bonds is much less than that absorbed by ductile tearing in a tough material, and this is why materials like ceramics and glasses are so brittle (see Figure 15.4). It is also why some steels become brittle and fail, like glass, at low temperatures—as we shall now explain.

At low temperatures metals having b.c.c. and c.p.h. structures become brittle and fail by cleavage, even though they may be tough at or above room temperature. In fact, only those metals with an f.c.c. structure (e.g., copper, lead, aluminum) remain unaffected by temperature in this way. In metals not having an f.c.c. structure, the motion of dislocations is assisted by the thermal agitation of the atoms (we shall talk in more detail about thermally activated processes in Chapter 22). At lower temperatures this thermal agitation is less, and the dislocations cannot move as easily as they can at room temperature in response to a stress—the intrinsic lattice resistance (Chapter 11) increases. The result is that the yield strength rises, and the plastic zone at the crack tip shrinks until it becomes so small that the fracture mechanism changes from ductile tearing to cleavage. This effect is called the ductile-to-brittle transition; for steels it can be as high as ≈0°C, depending on the composition of the steel; steel structures, such as ships, bridges, and oil rigs, are much more likely to fail in winter than in summer.

A somewhat similar thing happens in many polymers at the glass–rubber transition that we mentioned in Chapter 6. Below the transition these polymers are much more brittle than above it, as you can easily demonstrate by cooling a piece of rubber or polyethylene in liquid nitrogen. (Many other polymers, such as epoxy resins, have low K_c values at all temperatures simply because they are heavily cross-linked at all temperatures by covalent bonds and the material does not flow at the crack tip to cause blunting.)

15.4 Composites, Including Wood

As Figures 14.5 and 14.6 show, composites are tougher than ordinary polymers. The low toughness of materials, such as epoxy resins or polyester resins, can be enormously increased by reinforcing them with carbon fiber or glass fiber. But why is it that putting a second, equally (or more) brittle material such as graphite or glass into a brittle polymer makes a tough composite? The reason is the fibers act as crack stoppers (Figure 15.5).

The sequence in the figure shows what happens when a crack runs through the brittle matrix toward a fiber. As the crack reaches the fiber, the stress field just ahead of the crack separates the matrix from the fiber over a small region (a process called debonding) and the crack is blunted so much that its motion is arrested. Naturally, this only works if the crack is running normal to the fibers: wood is very tough across the grain, but can be split easily (meaning that K_c is low) along it.

One of the reasons why fiber composites are so useful in engineering design—in addition to their high stiffnesses that we talked about in Chapter 6—is their high toughness produced in this way. Of course, there are other ways of making polymers tough. The addition of small particles (“fillers”) of various sorts to polymers can modify their properties considerably.

Rubber-toughened polymers (e.g., ABS), for example, derive their toughness from the small rubber particles they contain. A crack intersects and stretches them as shown in Figure 15.6. The particles act as little springs, clamping the crack shut, and thereby increasing the load needed to make it propagate.

15.5 Avoiding Brittle Alloys

Let us finally return to the toughnesses of metals and alloys, as these are by far the most important class of materials for highly stressed applications. Even at, or above, room temperature, when nearly all common pure metals are tough, alloying of these metals with other metals or elements (e.g., with carbon to produce steels) can reduce the toughness. This is because alloying increases the resistance to dislocation motion (Chapter 11), raising the yield strength and causing the plastic zone to shrink. A more marked decrease in toughness can occur if enough impurities are added to make precipitates of chemical compounds formed between the metal and the impurities.

These compounds can often be very brittle and, if they are present in the shape of extended plates (e.g., sigma-phase in stainless steel; graphite in cast iron), cracks can spread along the plates, leading to brittle fracture. Finally, heat-treatments of alloys such as steels can produce different crystal structures having great hardness (but also therefore great brittleness because crack blunting cannot occur).

A good example of such a material is high-carbon steel after quenching into water from bright red heat: it becomes as brittle as glass. Proper heat treatment, following suppliers’ specifications, is essential if materials are to have the properties you want.

Worked Example

Underground tunnels in deep coal mines are usually supported by mine arches, made from curved lengths of steel I-beam bolted together on site. At the mine arch factory, straight lengths of I-beam stock were stored outside in the open, and were brought into the factory for punching bolt holes, bending to curve, and cutting to length. Fractures were common when the bending process was carried out in cold weather (steel temperature ≤ 0°C). This was disruptive and expensive—the bending process had to be stopped, then the broken I-beam had to be removed from the bending machine, and scrapped.

The following photographs show a typical fracture, from the edge of a punched hole, in the tensile part of the bending stress field. The fracture surface had the characteristics of a substantially brittle (cleavage) fracture:

• ▪ Essentially flat, with clear “chevron” markings pointing back to the fracture origin
  
• ▪ Perpendicular to the direction of tensile stress
  
• ▪ No significant plastic deformation—sharp edges, and no thinning down of the web

Once the first fracture occurred, further bending of the I-beam produced a tensile stress on the opposite side of the hole, which caused a second fracture. However, this fracture was a ductile shear fracture, with a fracture surface at 45° to the web surface (angle of maximum shear stress).

These brittle fractures are an excellent example of the ductile-to-brittle transition in b.c.c. steels. The change from a ductile to a cleavage fracture mechanism was caused by a combination of:

• ▪ Low temperature
  
• ▪ Considerable work-hardening at and near the bore of the hole, from the punching operation

Both make it harder for plastic flow to occur, and the cleavage stress is now less than the yield stress.

Examples

Answers