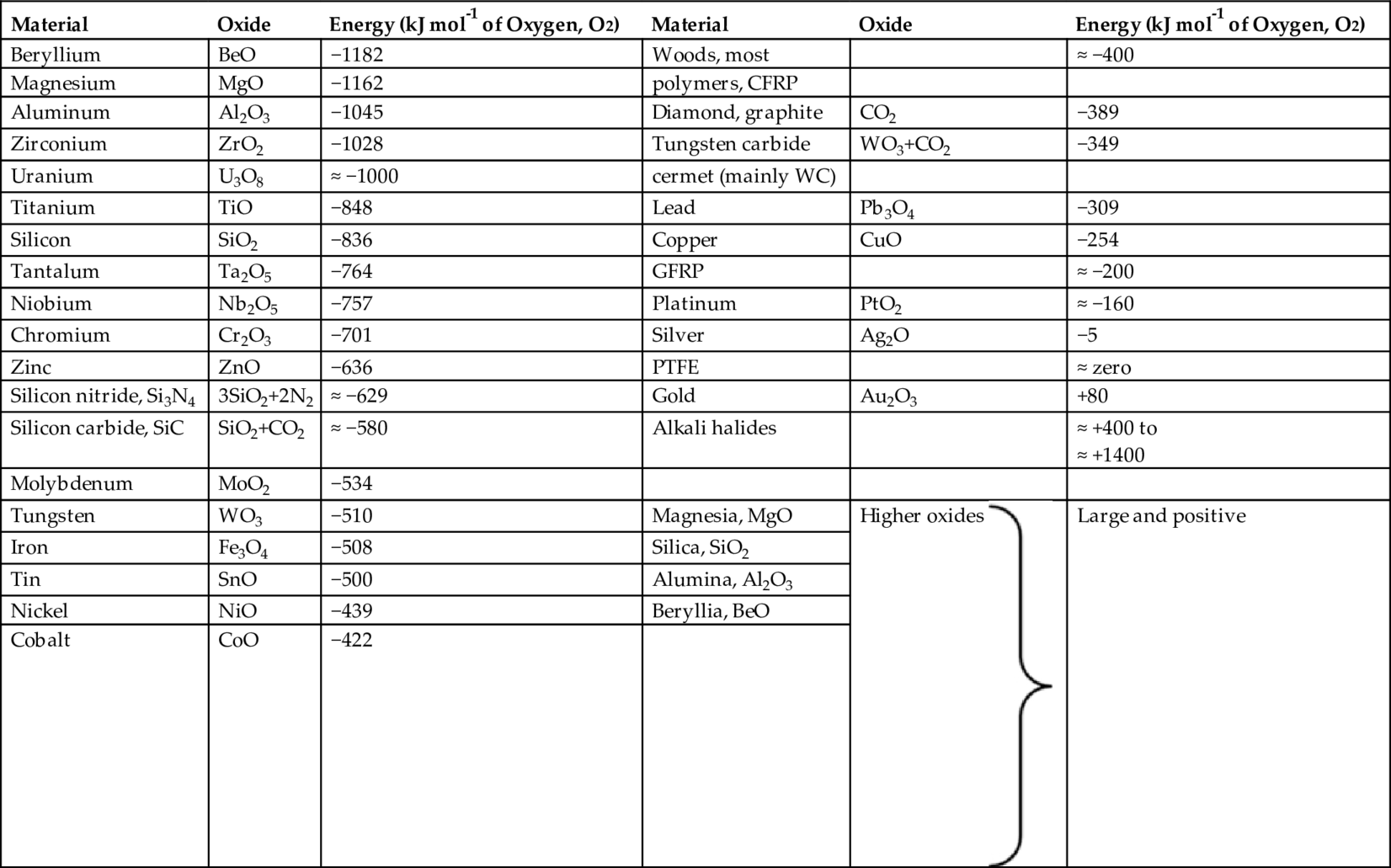
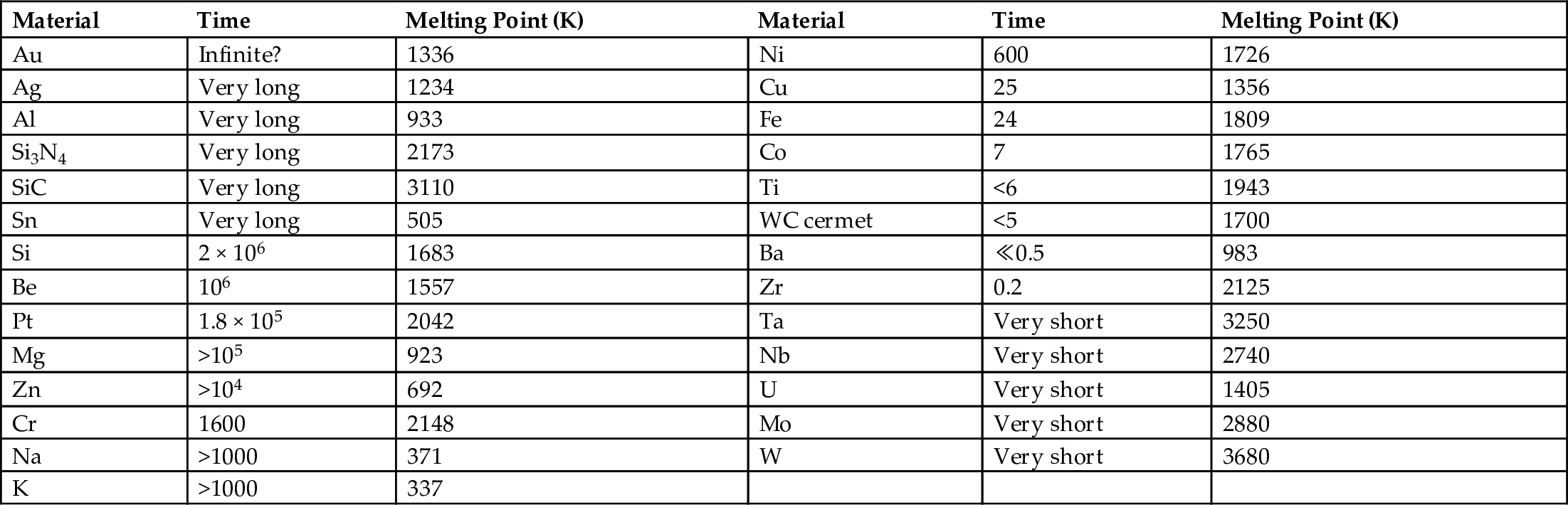
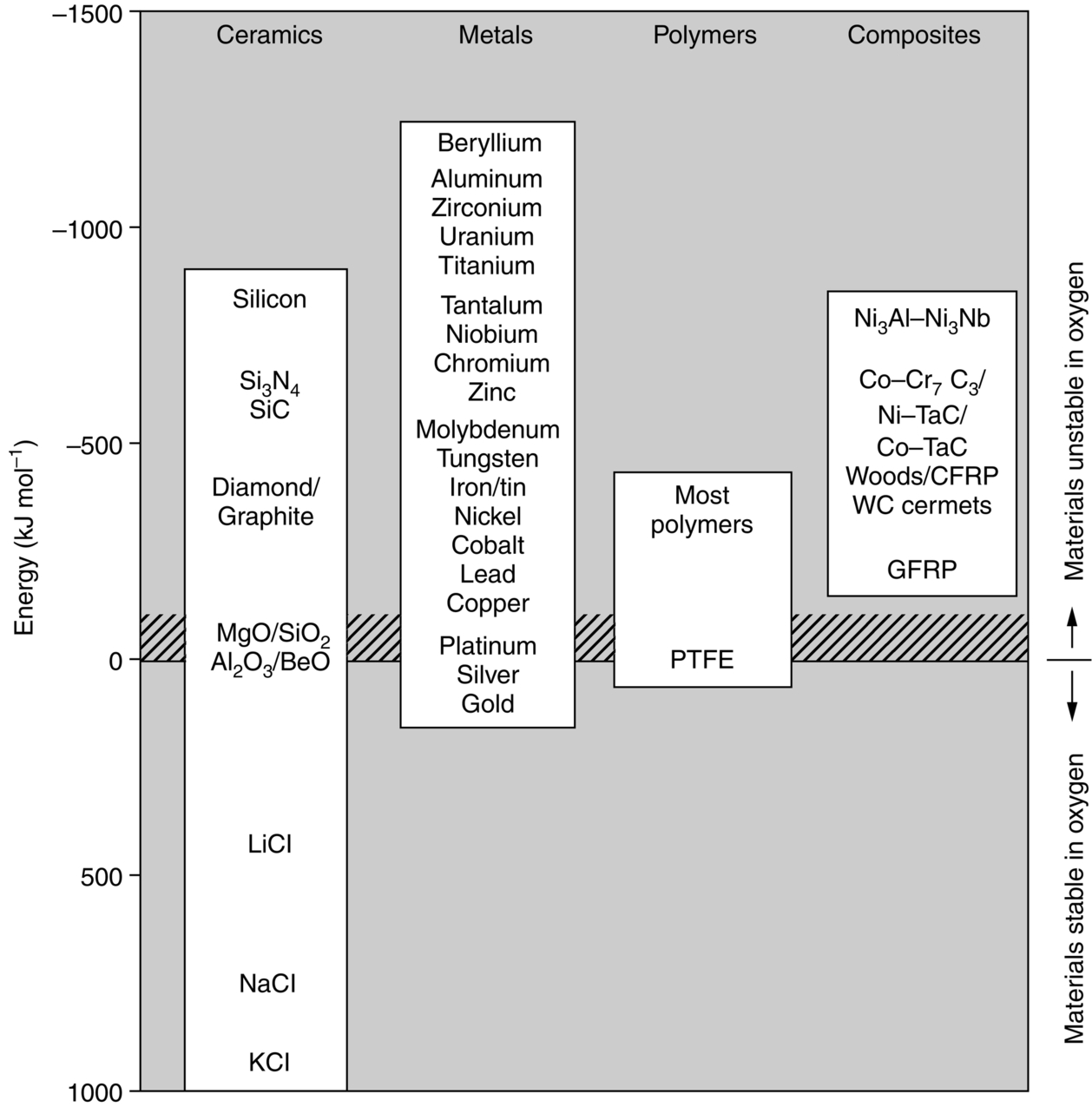
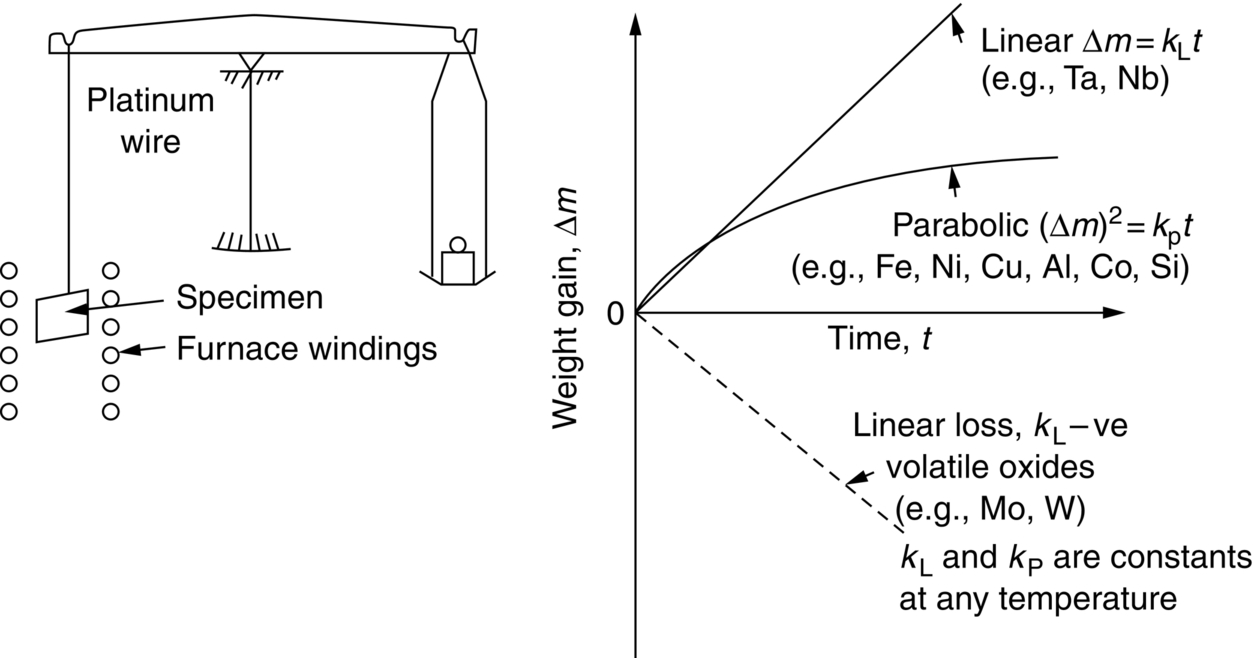
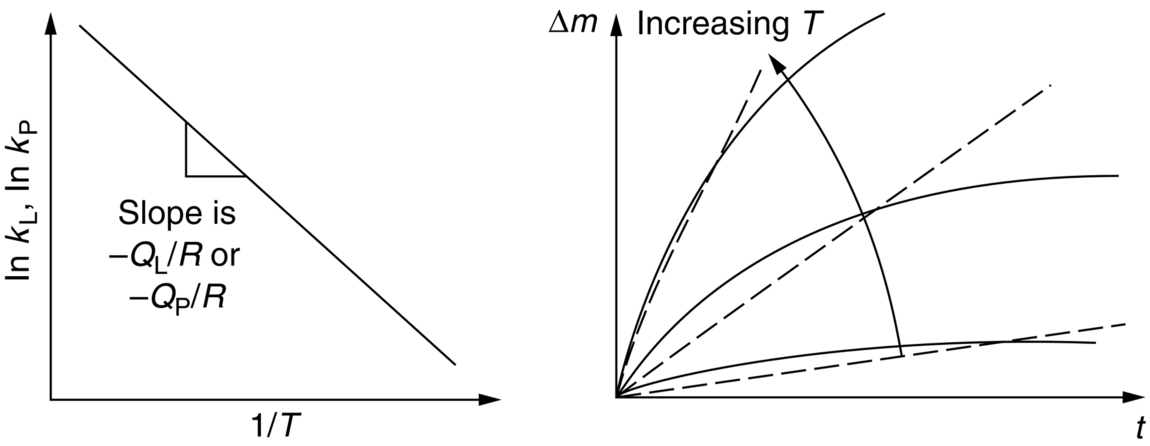
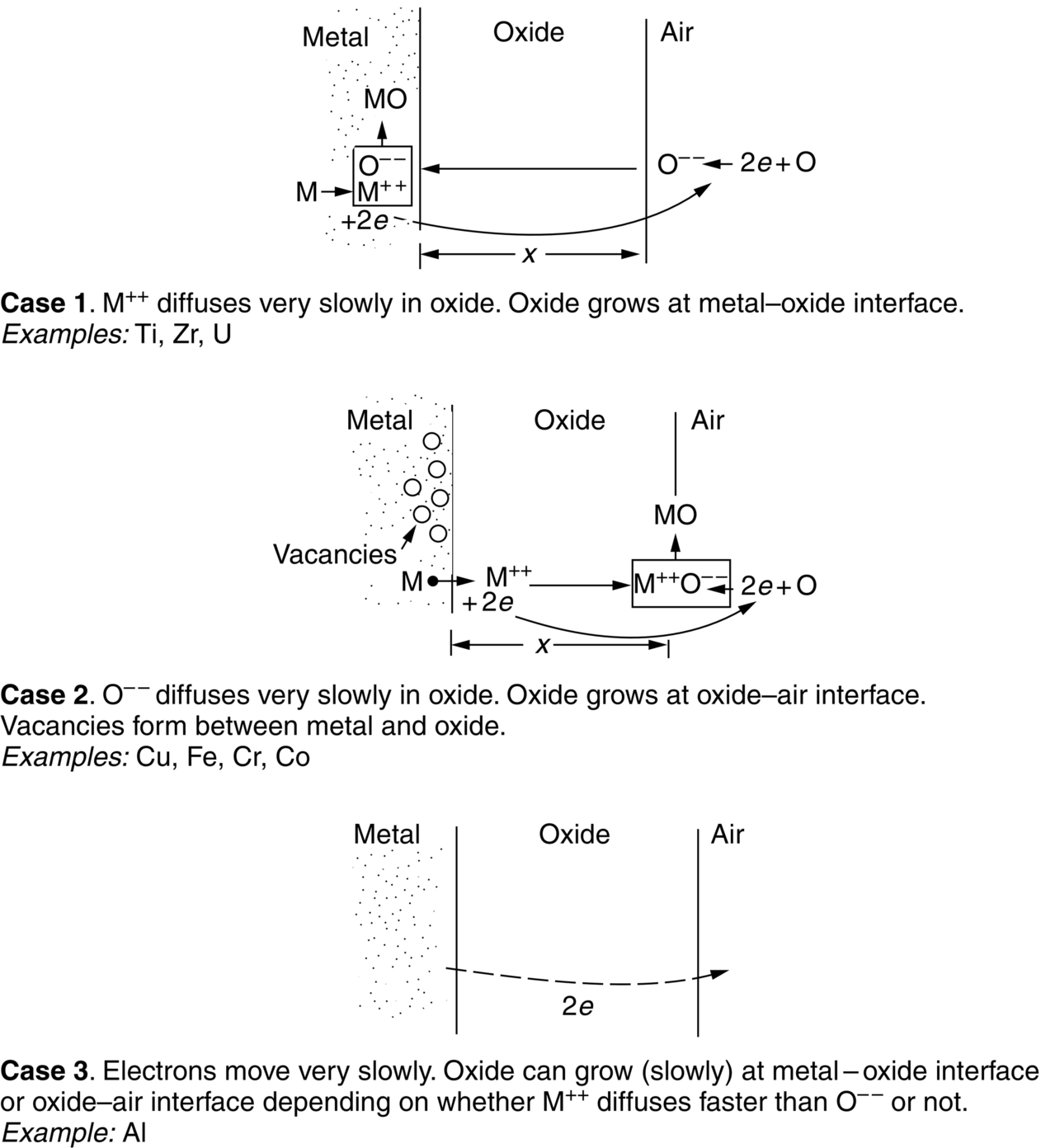
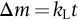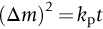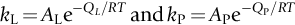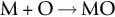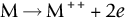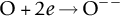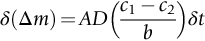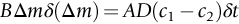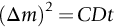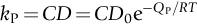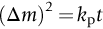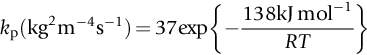section epub:type=”chapter”> One of the requirements of a high-temperature material—for example, in a turbine blade or a super-heater tube—is that it should resist attack by gases at high temperatures and, in particular, that it should resist oxidation. Turbine blades do oxidize in service and react with H2S, SO2, and other combustion products. Excessive attack of this sort is obviously undesirable in such a highly stressed component. This chapter answers various questions: Which materials best resist oxidation, and how can the resistance to gas attack be improved? The Earth’s atmosphere is oxidizing. By using the earth as a laboratory and looking for materials that survive well in its atmosphere, some idea of oxidation resistance can be obtained. The Earth’s crust is almost entirely made of oxides, silicates, aluminates, and other compounds of oxygen; and being oxides already, they are completely stable. Alkali halides, too, are stable: NaCl, KCl, and NaBr are widely found in nature. In contrast, metals are not stable: only gold is found in “native” form under normal circumstances; all the others in the data sheets will oxidize in contact with air. Polymers are not stable either as most of them may burn if ignited, meaning that they oxidize readily. Coal and oil are found in nature but that is only because geological accidents have sealed them off from all contact with air. In the last chapter we said that one of the requirements of a high-temperature material—in a turbine blade, or a super-heater tube, for example—was that it should resist attack by gases at high temperatures and, in particular, that it should resist oxidation. Turbine blades do oxidize in service, and react with H2S, SO2, and other combustion products. Excessive attack of this sort is obviously undesirable in such a highly stressed component. Which materials best resist oxidation, and how can the resistance to gas attack be improved? The earth’s atmosphere is oxidizing. We can get some idea of oxidation-resistance by using the earth as a laboratory, and looking for materials that survive well in its atmosphere. All around us we see ceramics: the earth’s crust (Chapter 2) is almost entirely made of oxides, silicates, aluminates, and other compounds of oxygen; and being oxides already, they are completely stable. Alkali halides, too, are stable: NaCl, KCl, NaBr—all are widely found in nature. By contrast, metals are not stable: only gold is found in “native” form under normal circumstances (it is completely resistant to oxidation at all temperatures); all the others in our data sheets will oxidize in contact with air. Polymers are not stable either: most will burn if ignited, meaning that they oxidize readily. Coal and oil (the raw materials for polymers), it is true, are found in nature, but that is only because geological accidents have sealed them off from all contact with air. A few polymers, among them PTFE (a polymer based on —CF2—), are so stable that they survive long periods at high temperatures, but they are the exceptions. And polymer-based composites, of course, are just the same: wood is not noted for its high-temperature oxidation resistance. This tendency of many materials to react with oxygen can be quantified by laboratory tests that measure the energy needed for the reaction If this energy is positive, the material is stable; if negative, it will oxidize. The bar-chart of Figure 25.1 shows the energies of oxide formation for our four categories of materials; numerical values are given in Table 25.1. When designing with oxidation-prone materials, it is obviously vital to know how fast the oxidation process is going to be. Intuitively one might expect that, the larger the energy released in the oxidation process, the faster the rate of oxidation. For example, one might expect aluminum to oxidize 2.5 times faster than iron from the energy data in Figure 25.1. In fact, aluminum oxidizes much more slowly than iron. Why should this happen? If you heat a piece of bright iron in a gas flame, the oxygen in the air reacts with the iron at the surface of the metal where the oxygen and iron atoms can contact, creating a thin layer of iron oxide on the surface, and making the iron turn black. The layer grows in thickness, quickly at first, and then more slowly because iron atoms now have to diffuse through the film before they make contact and react with oxygen. If you plunge the piece of hot iron into a dish of water the shock of the quenching breaks off the iron oxide layer, and you can see the pieces of layer in the dish. The iron surface now appears bright again, showing that the shock of the quenching has completely stripped the metal of the oxide layer which formed during the heating; if it were reheated, it would oxidize at the initial rate. The important thing about the oxide film is that it acts as a barrier which keeps the oxygen and iron atoms apart and cuts down the rate at which these atoms react to form more iron oxide. Aluminum, and most other materials, form oxide barrier layers in just the same sort of way—but the oxide layer on aluminum is a much more effective barrier than the oxide film on iron is. How do we measure rates of oxidation in practice? Because oxidation proceeds by the addition of oxygen atoms to the surface of the material, the weight of the material usually goes up in proportion to the amount of material that has become oxidized. This weight increase, Δm, can be monitored continuously with time t in the way illustrated in Figure 25.2. Two types of behavior are usually observed at high temperature. The first is linear oxidation, with where kL is a kinetic constant. Naturally, kL is usually positive. (In a few materials, however, the oxide evaporates away as soon as it has formed; the material then loses weight and kL is then negative.) The second type of oxidation behavior is parabolic oxidation, with where kp is another kinetic constant, this time always positive. Oxidation rates follow Arrhenius’s law (Chapter 22), that is, the kinetic constants kL and kp increase exponentially with temperature: AL and Ap, QL, and Qp are constants. As the temperature is increased, the rate of oxidation increases exponentially (Figure 25.3). Finally, oxidation rates obviously increase with increasing partial pressure of oxygen, although rarely in a simple way. The partial pressure of oxygen in a gas turbine atmosphere, for example, may well be very different from that in air, and it is important to conduct oxidation tests on high-temperature components under the right conditions. It is important from the design standpoint to know how much material is replaced by oxide. The mechanical properties of the oxide are usually grossly inferior to the properties of the material (e.g., oxides are comparatively brittle), and even if the layer is firmly attached to the material—which is certainly not always the case—the effective section of the component is reduced. The reduction in the section of a component can obviously be calculated from data for Δm. Table 25.2 gives the times for a range of materials required to oxidize them to a depth of 0.1 mm from the surface when exposed to air at 0.7TM (a typical figure for the operating temperature of a turbine blade or similar component): these times vary by many orders of magnitude, and clearly show that there is no correlation between oxidation rate and energy needed for the reaction (see Al, W for extremes: Al, very slow—energy = −1045 kJ mol−1 of O2; W, very fast—energy = −510 kJ mol−1 of O2). Figure 25.4 illustrates the mechanism of parabolic oxidation. The reaction (M is the oxidizing material and O is oxygen) goes in two steps. First M forms an ion, releasing electrons, e: These electrons are then absorbed by oxygen to give an oxygen ion: The process involves the diffusion of ions and the conduction of electrons through the oxide layer. There are three ways in which this can occur — see Figure 25.4, Case 1, Case 2 and Case 3. As we saw in Chapter 22 (Equation (22.2)), diffusion is described by Fick’s first law where J is the flux of atoms (or ions)—the number of atoms/ions diffusing down the concentration gradient per second per unit area, D is the diffusion coefficient (D = D0e–Q/RT), x is distance along the flux lines, and c is the concentration of atoms/ions—the number of atoms/ions per unit volume. In the case of oxidation, the flux consists of ions of either M++ or O− −, depending on which of these is the rate-determining ion. The rate of oxidation is obviously proportional to the flux of ions, so in a time δt the mass gain δ(Δm) = AJδt, where A = constant. The concentration gradient of M++ or O− − is (c1 – c2)/b, where c1 and c2 are the ion concentrations on either side of the oxide layer, and b is the thickness of the layer. So, from Fick’s law, Now as oxidation proceeds, the oxide layer grows, from zero thickness initially to b after time t. So b = B(Δm), where B = constant. Then We integrate from Δm = 0 to Δm = Δm, and t = 0 to t = t. We assume that c1 and c2 are both constant. Then where C = constant. This growth law has exactly the same form as Equation (25.2), with kinetic constant This is the same as Equation (25.3), with the parabolic constant AP = CD0. This shows us why some films are more protective than others: protective films are those with low diffusion coefficients—and thus high melting points. That is one reason why Al2O3 protects aluminum, Cr2O3 protects chromium, and SiO2 protects silicon so well, whereas Cu2O and even FeO (which have lower melting points) are less protective. But there is an additional reason: electrons must also pass through the film and these films are insulators (the electrical resistivity of Al2O3 is 109 times greater than that of FeO). Although our simple oxide film model explains most of the experimental observations we have mentioned, it does not explain the linear laws. How, for example, can a material lose weight linearly when it oxidizes as is sometimes observed (see Figure 25.2)? Well, some oxides (e.g., MoO3, WO3) are very volatile. During oxidation of Mo and W at high temperature, the oxides evaporate as soon as they are formed, and offer no barrier at all to oxidation. Oxidation, therefore, proceeds at a rate that is independent of time, and the material loses weight because the oxide is lost. This behavior explains the catastrophically rapid section loss of Mo and W shown in Table 25.2. The explanation of a linear weight gain is more complex. Basically, as the oxide film thickens, it develops cracks, or partly lifts away from the material, so the barrier between material and oxide does not become any more effective as oxidation proceeds. Figure 25.5 shows how this can happen. If the volume of the oxide is much less than that of the material from which it is formed, it will crack to relieve the strain (oxide films are usually brittle). If the volume of the oxide is much greater, on the other hand, the oxide will tend to release the strain energy by breaking the adhesion between material and oxide, and springing away. For protection, then, we need an oxide skin that is neither too small and splits open (like the bark on a fir tree) nor one that is too big and wrinkles up (like the skin of an elephant), but one which is just right. Then, and only then, do we get protective parabolic growth.
Oxidation of Materials
Publisher Summary
25.1 Introduction
25.2 Energy of Oxidation
25.3 Rates of Oxidation
25.4 Data
25.5 Micromechanisms

Examples
Answers