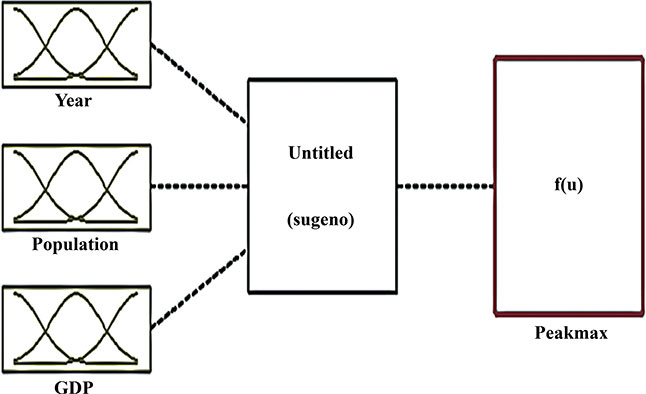
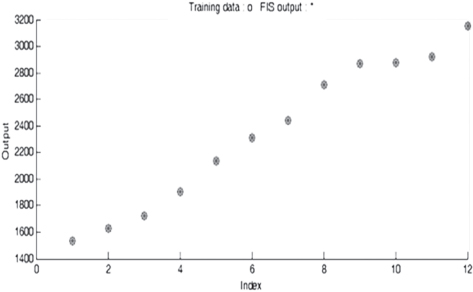
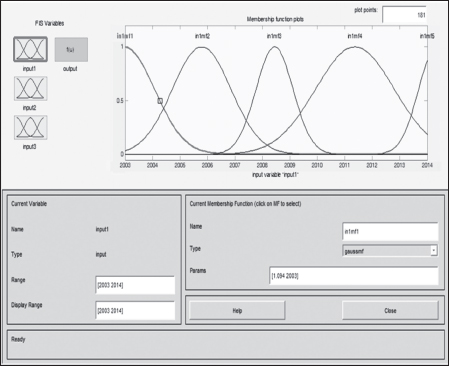
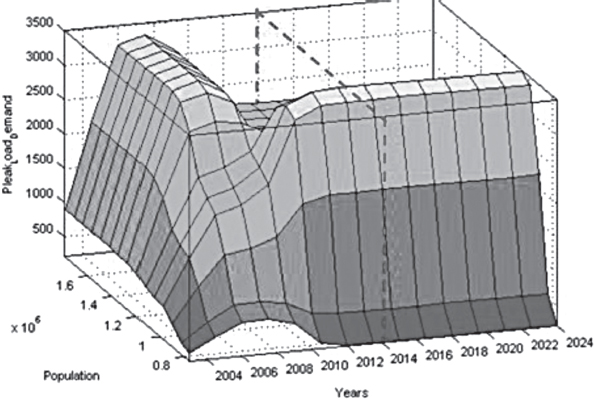
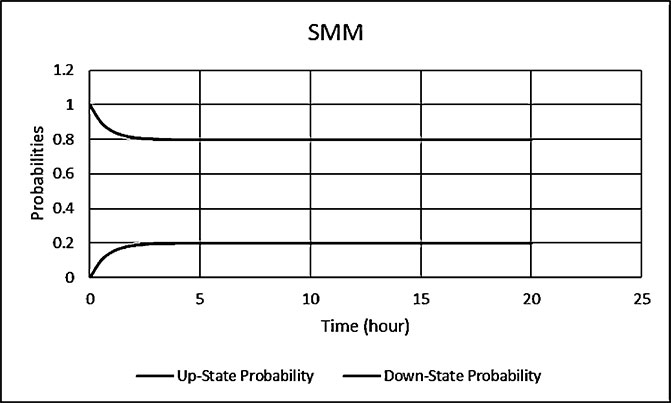
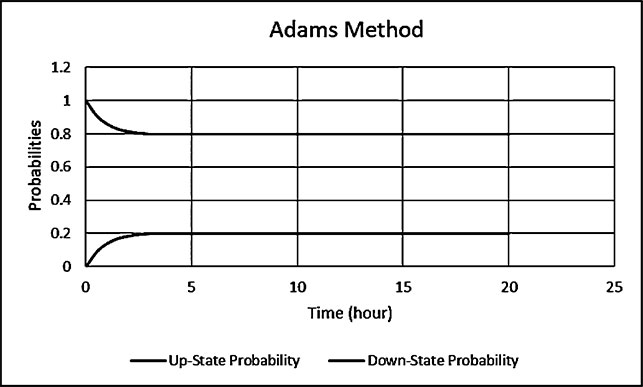
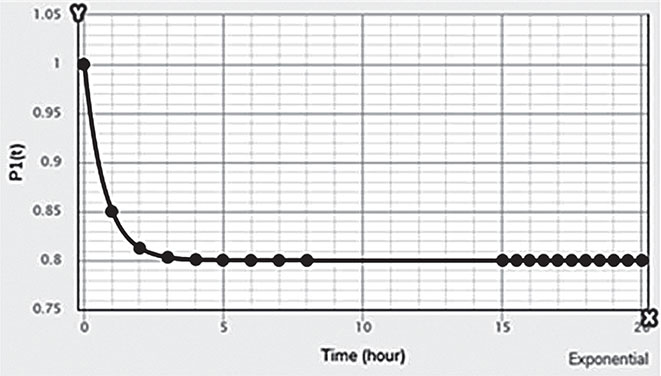
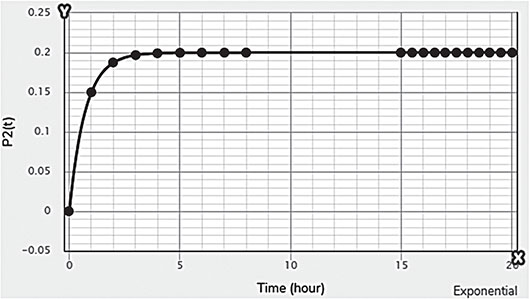
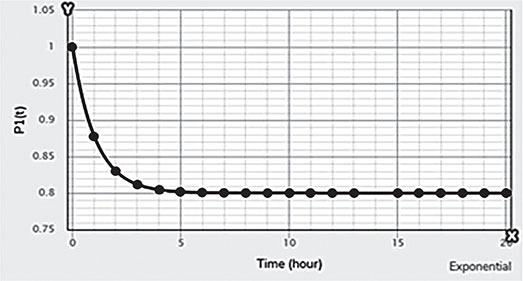
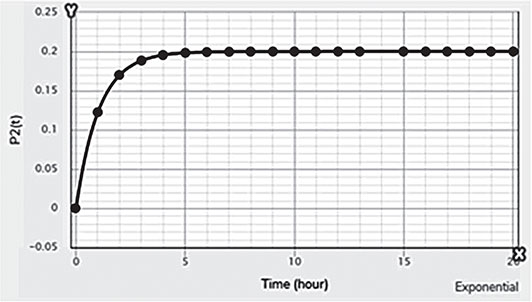
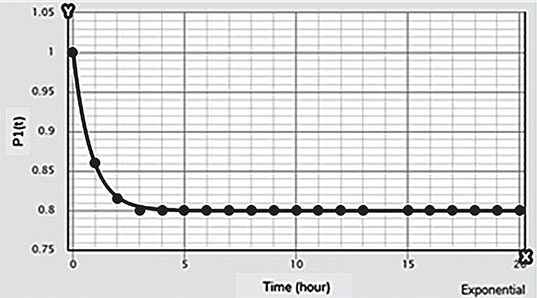
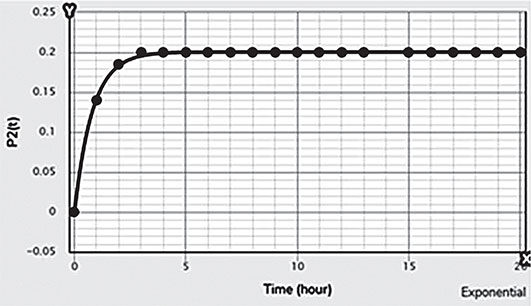
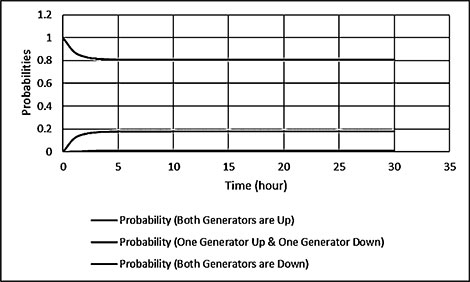
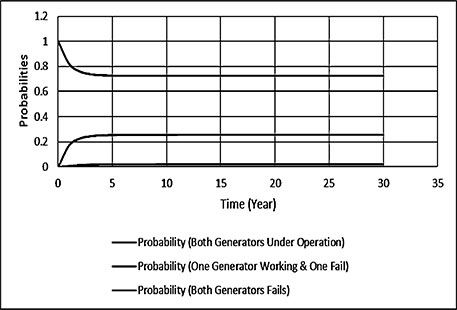
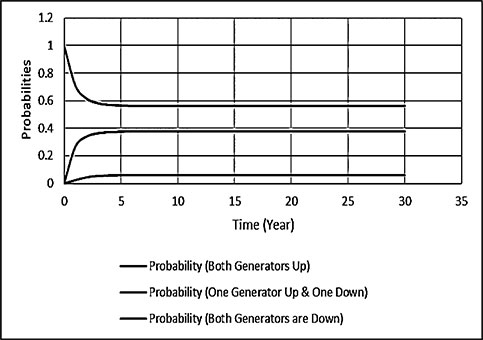
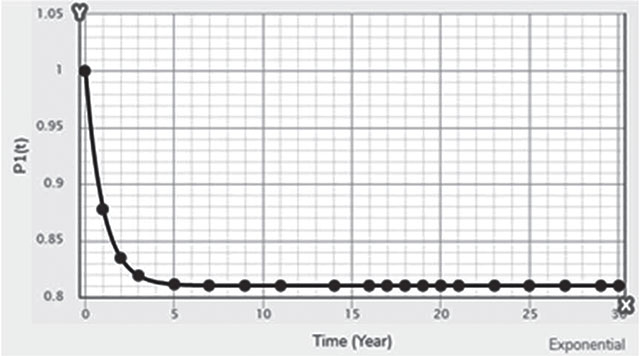
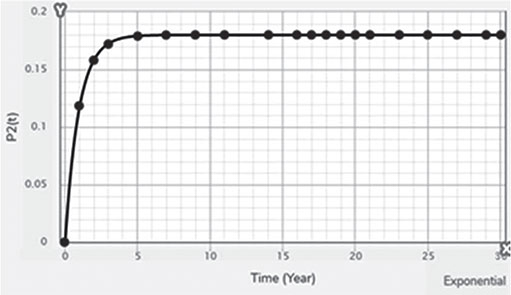
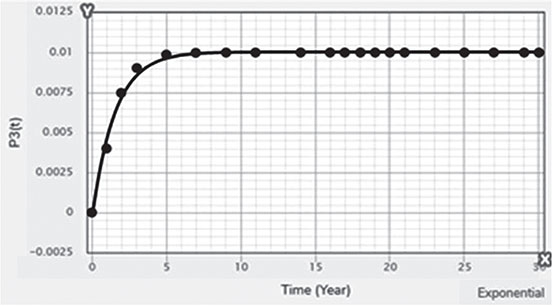
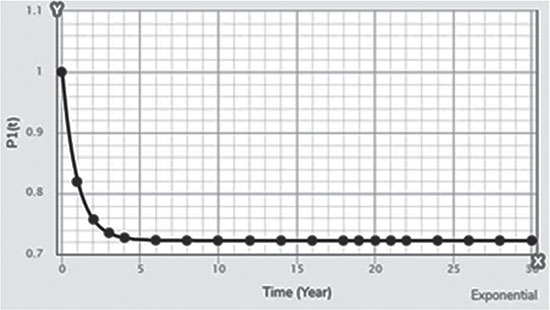
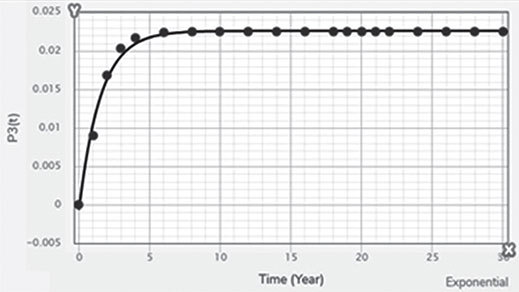
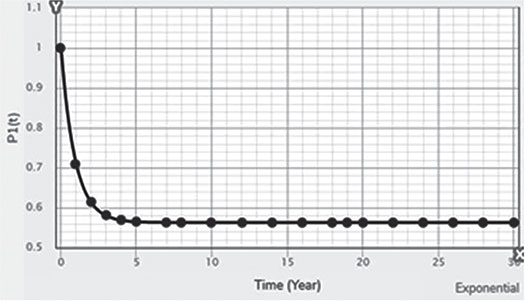
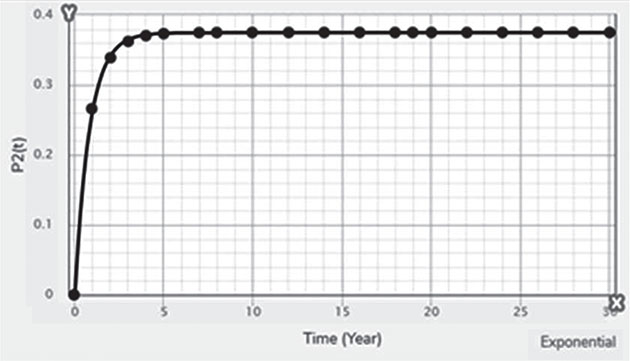
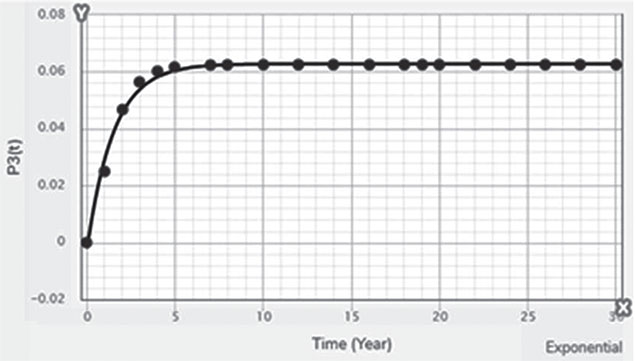
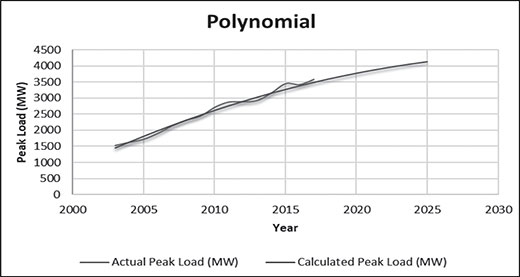
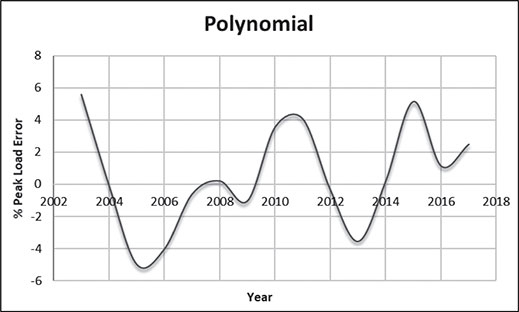
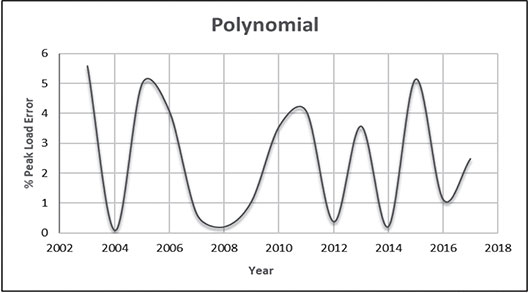
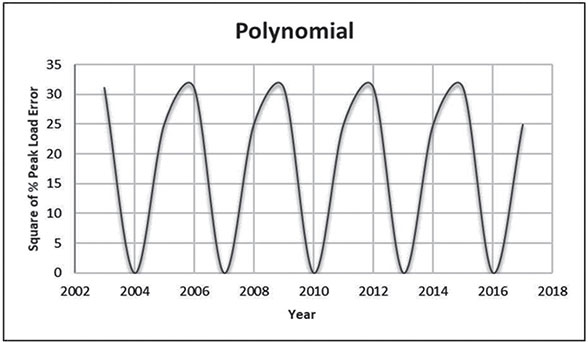
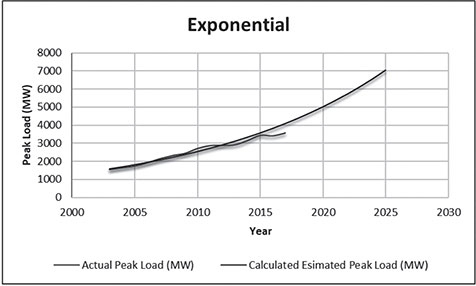
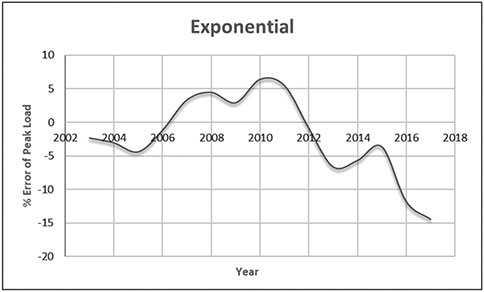
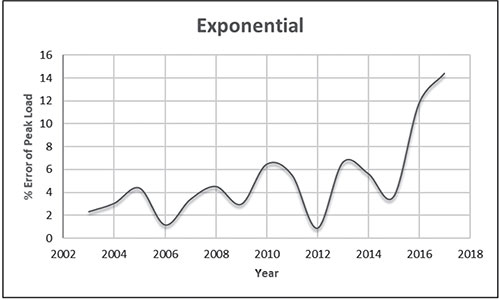
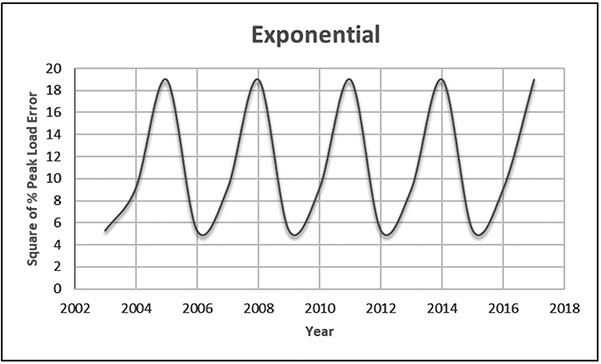
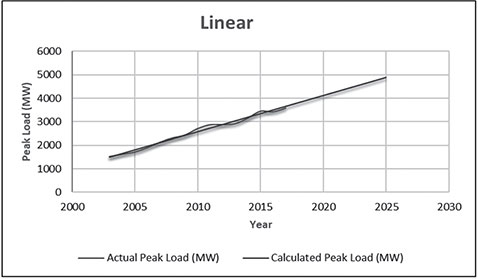
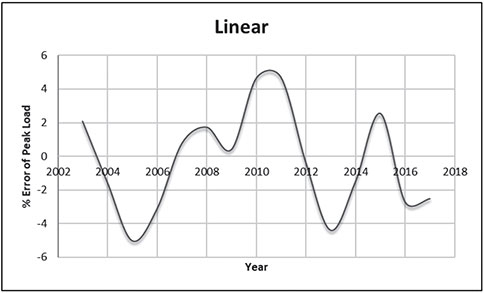
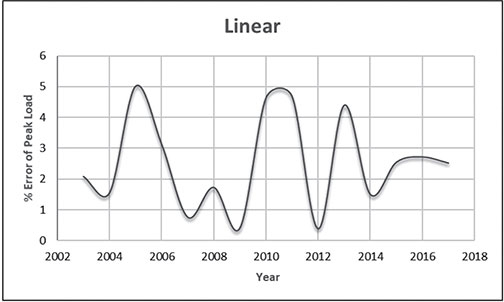
Electrical energy is an essential ingredient for the development of modern society. Almost all aspects of daily life depend on the use of electrical energy and the performance of a power utility. The power utility is measured in terms of the quality and reliability of the supply. Electric power utilities have invested a substantial amount of capital in generating stations, transmission lines, and distribution facilities to supply electrical energy to their customers as economically as possible and with a reasonable assurance of continuity, safety, and quality. This creates the difficult problem of balancing the need for continuity of power supply with the costs involved. There are a number of methods for constructing the transition rate matrix. For general systems using the Kronecker algebra helps to form a transition rate matrix. This is one method out of a number of methods that help to form a transition rate matrix. Also, the rules and properties can be introduced. The Kronecker algebra is used in this textbook for constructing the transition rate matrix of a system contain a number of power stations. The two-state model refers to a generator passing through two-states. In this case, the power generator is passing through Up-State and Down-State. This means the generator is operating and is failing, respectively. The three methods to calculate the transient probabilities for the considered system are discussed earlier in Chapter 8. The results are obtained using the SMM illustrated in Table 10.1 and Figure 10.1. Table 10.2 and Figure 10.2 illustrate the results obtained by the Rung-Kutta method. Finally, Table 10.3 and Figure 10.3 show the results obtained by the Adams method. These three methods are recommended to calculate the transient and steady-state probabilities for any model. Time (year) P1(t) P2(t) 0 1 0 0.5 0.9 0.1 1 0.85 0.15 1.5 0.825 0.175 2 0.8125 0.1875 2.5 0.8063 0.1938 3 0.8031 0.1969 3.5 0.8016 0.1984 4 0.8008 0.1992 4.5 0.8004 0.1996 5 0.8002 0.1998 5.5 0.8001 0.1999 6 0.8 0.2 6.5 0.8 0.2 7 0.8 0.2 7.5 0.8 0.2 8 0.8 0.2 15 0.8 0.2 15.5 0.8 0.2 16 0.8 0.2 16.5 0.8 0.2 17 0.8 0.2 17.5 0.8 0.2 18 0.8 0.2 18.5 0.8 0.2 19 0.8 0.2 19.5 0.8 0.2 20 0.8 0.2 Time (year) P1(t) P2(t) 0 1 0 0.5 0.9245 0.0755 1 0.8775 0.1225 1.5 0.8482 0.1518 2 0.83 0.17 2.5 0.8187 0.1813 3 0.8116 0.1884 3.5 0.8072 0.1928 4 0.8045 0.1955 4.5 0.8028 0.1972 5 0.8017 0.1983 5.5 0.8011 0.1989 6 0.8007 0.1993 6.5 0.8004 0.1996 7 0.8003 0.1997 7.5 0.8002 0.1998 8 0.8001 0.1999 8.5 0.8001 0.1999 9 0.8 0.2 9.5 0.8 0.2 10 0.8 0.2 10.5 0.8 0.2 11 0.8 0.2 11.5 0.8 0.2 12 0.8 0.2 12.5 0.8 0.2 13 0.8 0.2 13.5 0.8 0.2 14 0.8 0.2 14.5 0.8 0.2 15 0.8 0.2 15.5 0.8 0.2 16 0.8 0.2 16.5 0.8 0.2 17 0.8 0.2 17.5 0.8 0.2 18 0.8 0.2 18.5 0.8 0.2 19 0.8 0.2 19.5 0.8 0.2 20 0.8 0.2 Time (hr) P1(t) P2(t) 0 1 0 0.5 0.91 0.09 1 0.86 0.14 1.5 0.83 0.17 2 0.815 0.185 2.5 0.805 0.195 3 0.8 0.2 3.5 0.8 0.2 4 0.8 0.2 4.5 0.8 0.2 5 0.8 0.2 5.5 0.8 0.2 6 0.8 0.2 6.5 0.8 0.2 7 0.8 0.2 7.5 0.8 0.2 8 0.8 0.2 8.5 0.8 0.2 9 0.8 0.2 9.5 0.8 0.2 10 0.8 0.2 11 0.8 0.2 11.5 0.8 0.2 12 0.8 0.2 13 0.8 0.2 14 0.8 0.2 15 0.8 0.2 16 0.8 0.2 17 0.8 0.2 18 0.8 0.2 19 0.8 0.2 20 0.8 0.2 The curve fitting technique, applied to the three methods, is used to find out the results for the two-state model. The results are illustrated in Figures 10.4a, b using SMM, Figures 10.5a, b using the Runge-Kutta method, and Figures 10.6a, b using Adams method. The suitable equations for the three methods are summarized in Table 10.4. The three-state model (Figure 10.7) is considered for a case of two generators under operation in a power station. The first state considered that both generators are working, where the second state illustrates that one is working and the others fail. In the third state, both generators are in a failstate. Using the Laplace transforms will result: Method Probability a b c SMM 1 0.7999963±0.000003416 0.2000039±0.00001428 1.386269±0.0002655 2 0.2000037±0.000003416 –0.2000039±0.00001428 1.386269±0.0002655 Runge-Kutta 1 0.7999955±0.000005142 0.2000096±0.00002047 0.948314±0.000219 2 0.2000045±0.000005142 –0.2000096±0.00002047 0.948314±0.000219 Adams 1 0.7996066±0.0003309 0.2007632±0.001368 1.236986±0.02122 2 0.2003934±0.0003309 –0.2007631±0.001368 1.236985±0.02122 The results are illustrated in three cases. These cases are summarized in Tables 10.5, 10.6, 10.7, 10.8 and Figures 10.8, 10.9, 10.10. Case # μ (per year) λ (per year) Table Figure 1 0.9 0.1 2 0.85 0.15 3 0.75 0.25 TIME (YEAR) P1(T) P2(T) P3(T) 0 1 0 0 1 0.877571652 0.118432584 0.003995764 2 0.834543507 0.157980042 0.007476451 3 0.81898646 0.171984494 0.009029046 4 0.81330017 0.177062789 0.009637042 5 0.811213284 0.17892102 0.009865695 6 0.810446237 0.179603277 0.009950486 7 0.810164147 0.179854082 0.009981771 8 0.810060384 0.179946324 0.009993292 9 0.810022214 0.179980254 0.009997532 10 0.810008172 0.179992736 0.009999092 11 0.810003006 0.179997328 0.009999666 12 0.810001106 0.179999017 0.009999877 13 0.810000407 0.179999638 0.009999955 14 0.81000015 0.179999867 0.009999983 15 0.810000055 0.179999951 0.009999994 16 0.81000002 0.179999982 0.009999998 17 0.810000007 0.179999993 0.009999999 18 0.810000003 0.179999998 0.01 19 0.810000001 0.179999999 0.01 20 0.81 0.18 0.01 21 0.81 0.18 0.01 22 0.81 0.18 0.01 23 0.81 0.18 0.01 24 0.81 0.18 0.01 25 0.81 0.18 0.01 26 0.81 0.18 0.01 27 0.81 0.18 0.01 28 0.81 0.18 0.01 29 0.81 0.18 0.01 30 0.81 0.18 0.01
CHAPTER 10
Power Systems Reliability Applications
10.1 INTRODUCTION
10.2 EQUIVALENT TRANSITION RATE MATRIX
10.3 TWO-STATE MODEL
10.4 THREE-STATE MODELS
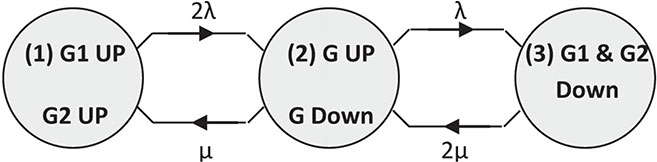
Source: Modified from Billinton and Allan, 1992.