Any system under study needs a transient study status. For this reason, the problem of obtaining transient probabilities solution addressed in the present chapter. Going through this type of study is helping to find not only the transient solution, but also the steady-state probabilities for the overall electric power system. The transient solution is necessary, where the importance came from the role of the transient solution in studying the behavior of power system model immediately after start-up or repairs the system, or even the behavior is needed over a certain limit period through which the system is required to perform a given mission (Thomson, 1018). To obtain the transient solution, there are many methods to find the solution of the electric power system discussed in the literature. However, in the present chapter, three different methods are discussed and studied. These three are: • Fourth order Runge-Kutta method. • System multiplication method (SMM). • Adams method (using Matlab Simulink). The aim of this chapter is to show how transient probabilities for any model can be conveniently obtained numerically. The German mathematicians Carl Runge (1856–1927) and Wilhelm Kutta (1867–1944) the Runge-Kutta method was introduced the fourth-order method, which is widely used in much present-day computer application (Thomson, 2018). The reason behind that is the computation speed, precision, and relatively large interval of stability (Tang, 2018). The algorithms for the method popularly known simply as Rung-Kutta method which can be written as follows: where: i is the i iteration number (i = 1 to n).; j is the function number (j = 1 to N).; i and j are integers. In Tang’s (2018) study, the author developed two ways to construct Runge-Kutta type methods of a randomly high order. In the construction of Runge-Kutta type methods, a critical technique associated with the orthogonal polynomial expansion is applied. By using this approach, we do not need to study the simple solution of multivariable nonlinear algebraic equations restricting from order conditions. The author (Tang, 2018) provides a note on continuous-stage Runge-Kutta methods (csRK) for solving initial value problems of first-order ordinary differential equations. These methods are an interesting and creative extension of traditional Runge-Kutta methods, it can give us a new perspective on Runge-Kutta discretization, and it may enlarge the application of its approximation theory in modern mathematics and engineering fields. A highlighted advantage of the investigation of csRK methods that it does not need to study the tedious solution of multivariable nonlinear algebraic equations associated with order conditions. At the same time, the author review, discuss, and further promote the recently-developed csRK theory. In the construction of RK-type methods, a crucial technique associated with the orthogonal polynomial expansion is fully utilized. By using this approach, we do not need to study the tedious solution of multivariable nonlinear algebraic equations stemming from order conditions. The classical continuous Runge-Kutta methods are widely applied to compute the numerical solutions of delay differential equations without impulsive perturbations. However, the classical continuous Runge-Kutta methods cannot be applied directly to impulsive delay differential equations, because the exact solutions of the impulsive delay differential equations are not continuous. In Zhang and Song (2019) study they impulsive continuous Runge-Kutta methods which are constructed for impulsive delay differential equations with the variable delay based on the theory of continuous Runge-Kutta methods, convergence of the constructed numerical methods is studied, and some numerical examples are given to confirm the theoretical results (Christopher et al., 2019). Two new implicit-explicit additive Runge-Kutta (ARK2) methods are given with fourth-and fifth-order formal accuracies, respectively. Both methods are in (Kennedya, Mark, and Carpenterb, 2019). Both methods are combining explicit Runge-Kutta (ERK) methods with explicit singly-diagonally implicit Runge-Kutta (ESDIRK) methods and include an embedded method for error control. The two methods have ESDIRKs that are internally L-stable on stages three and higher, have only modestly negative Eigenvalues to the stage and step algebraic-stability matrices, and have stage-order two. To improve computational efficiency, the fourthorder method has a diagonal coefficient of 0.1235. This is concluding to offset much of the extra computational cost of an extra stage by facilitating iterative convergence at each stage. Linear stability domains for both ERK methods have been made quite large, and the dominant coupling stability term between the stability of the ESDIRK and ERK for very stiff modes has been removed. As well, the fourth-order method is one of the best all-around fourth-order IMEX ARK2, which the authors are aware of. The fifth-order method is likely best suited to mildly stiff problems with tight error tolerances. The methods were tested. The obtained results suggested that these new methods represent an improvement over existing methods of the same class. In many existed practical problems, a natural unit of time often suggested itself, i.e., if a person modeling the behavior of weather, a convenient unit of time could be a week. This natural discrimination of time also often has an advantage in numerical evaluation (Thomson, 2018). The transformation from the continuous-time to the discrete-time domain can be accomplished as follows by considering: where A is the transition rate matrix. One can approximate the differentiation of the probability as a function of time to the rate of time as: The variable h is a sufficiently small interval of time. To study any system, the researcher assumed the variable (h) as an interval. Nevertheless, this gives: i.e., where T is called a transition matrix defined now by: and I is the unit matrix. Therefore, the algorithm for the present method can be written as follows: The technique called the Adams method (Ameen, and Novati, 2017) is used to find the numerical solutions of initial value problems. The effectiveness of this technique is helping for the treatment of problems based on its attractive properties and an efficient technique. It deals with the algebraic nonlinear systems. The Adams method is a predictor-corrector and multi-step method. The principle behind using this method is the use of the past calculated values of P(t) to build a polynomial that approximates the derivative function and extrapolate this into the next interval (Yanga and Ralescu, 2015). The general formula of the Adams method is as follows: and where Elimination of error terms gives the formula: The SMM, Runge-Kutta, and Adams methods are compared, and the way of obtaining solutions of prescribed accuracy is outlined for the methods which numerically integrate the differential equation. The step length used determines the accuracy of the integration methods, and so it is useful to be able to estimate the step length to give the required accuracy. In principle, the step length is determined by calculating two rough estimates of the solution and using them to determine the final step length. For some p ≥ 1, the error is 0(hp). So, to estimate a suitable h, the following procedure is adopted: Let x be the true value to be estimated. Using step size h1 to obtain an estimate value r1. Using step size h2 to obtain an estimate value r2. Suppose the errors are e1 and e2, respectively, where: e1 = zh1p Then the estimated values are: Divide step size h1 by n (an integer) to obtain h2. Then where n is the step error. Now |r1–r2| = |e1-e2| Therefore, the factor z is the same for all the estimated values. Choosing h3 = h1/l and following the same procedure as above for h2, it’s found that: Then Since h1 and l are known, h3 will be h3 = h1/l.
CHAPTER 8
Transient Probabilities Solution
8.1 INTRODUCTION
8.2 FOURTH-ORDER RUNGE-KUTTA METHOD
8.3 SYSTEM MULTIPLICATION METHOD (SMM)
8.4 ADAMS METHOD
8.5 INCREMENTAL OF TIME LIMITATION (H)
8.6 SYSTEM COMBINATION
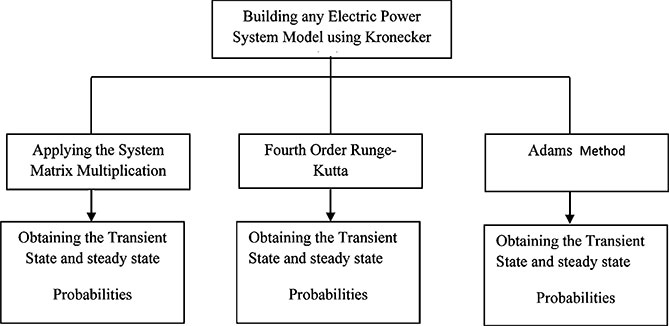
The SMM, Runge-Kutta, and Adams methods are forming an easy method to help in calculating the steady-state and transient probabilities of any electric power system model. A program for calculating the transient state probabilities was obtained, as illustrated in Figure 8.1. At the same time, the steady-state probabilities are obtained through the transient solution. The combination of the presented methods is combined with the methods presented in Chapter 7.
KEYWORDS
• additive Runge-Kutta
• explicit Runge-Kutta
• explicit, singly-diagonally implicit Runge-Kutta
• system multiplication method
REFERENCES
Ameen, I., & Novati, P. The solution of fractional order epidemic model by implicit Adams methods. Applied Mathematical Model, 2017, 43, 78–84.
Christopher, A. Kennedy, C. A., & Carpenter, M. H. Higher-order additive Runge–Kutta schemes for ordinary differential equations. International Journal on Applied Numerical Mathematics, 2019, 136, 183–205.
Kennedya, C. A., Mark, H., & Carpenterb, M. H. Higher-order additive Runge–Kutta schemes for ordinary differential equations. Applied Numerical Mathematics, 2019, 136, 183–205.
Tang, W. A Note on continuous-stage Runge-Kutta methods. International Journal on Applied Mathematics and Computation, 2018, 339, 231–241.
Thomson, W. T. Theory of Vibration with Applications (4th edn.). 2018, Taylor and Francis, New York.
Yanga, X., & Ralescu, D. Adams method for solving uncertain differential equations. Applied Mathematics and Computation, 2015, 270, 993–1003.
Zhanga, G., & Song, M. Impulsive continuous Runge-Kutta methods for impulsive delay differential equations. International Journal on Applied Mathematics and Computation, 2019, 341, 160–173.