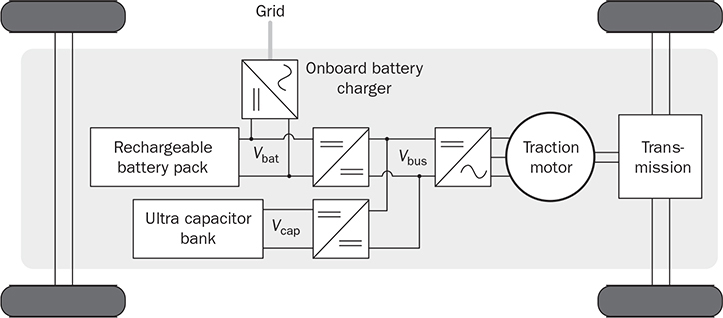
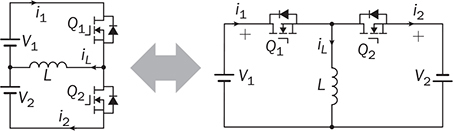
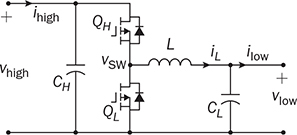
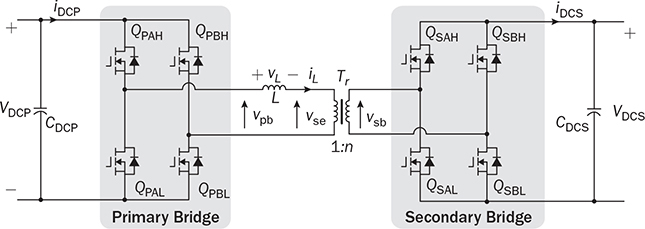
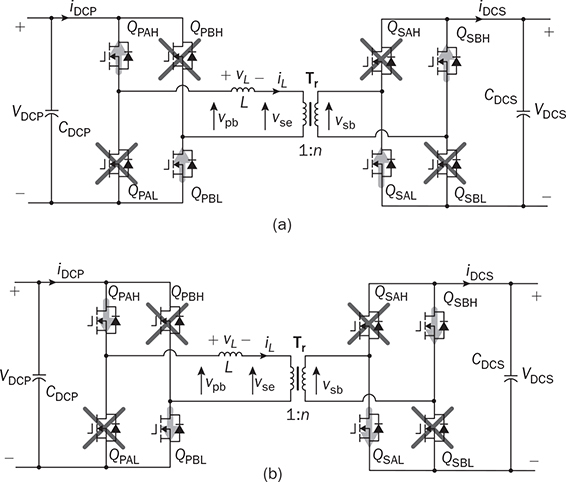
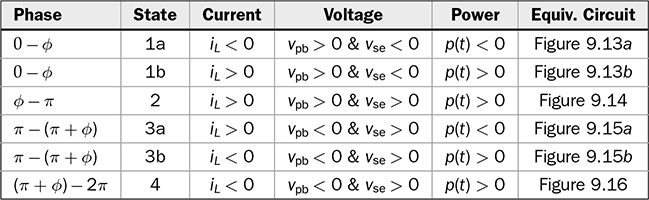
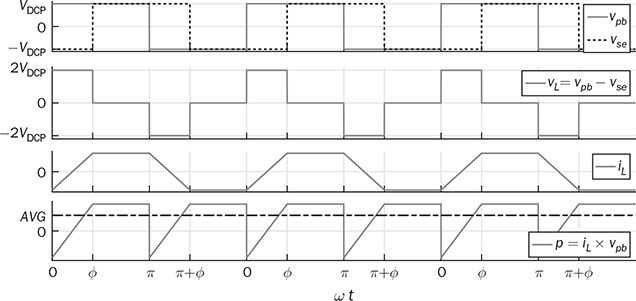
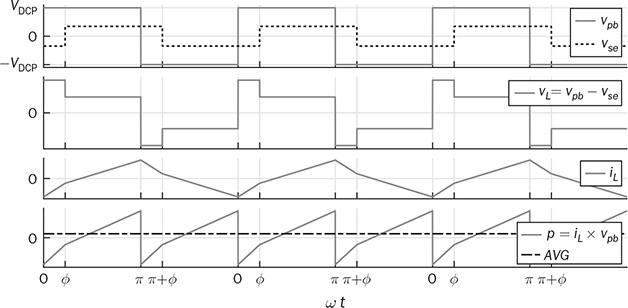
The discussion in previous chapters focused on the unidirectional converters. The power source and load can be clearly distinguished to identify the active power flow direction. According to the classification in Sec. 1.1, another group of power conversion is bidirectional, applications of which are increasing because of the large utilization of rechargeable batteries for electrical vehicles (EVs) and grid interconnection. Power transformers can support voltage conversion and bidirectional power flow in a passive way. The latest applications are based on power converters to control the bidirectional power flow. Figure 9.1 demonstrates one system configuration to operate an EV. FIGURE 9.1 Diagram example of electric vehicle. When the EV is running at the nominal condition, the power source is the rechargeable battery pack to supply active power to the DC bus, Vbus. The ultracapacitor bank can be discharged to support short-term power in case the vehicle accelerates. The DC/AC stage drives the traction motor to rotate. When the vehicle goes for a long downhill, the motor can become a generator to produce braking power. The regenerated power should be through the AC/DC path and inject to the DC bus. Meanwhile, the battery and ultracapacitor units should be charged via the bidirectional DC/DC converters to store the braking energy. The four power converters shown in Fig. 9.1 shall be bidirectional to operate the EV efficiently. Following the smart grid concept, future EVs should participate in power management and grid support. When a single converter is used for interfacing rechargeable batteries, bidirectional power conversion is required. An equalizing process is generally required to avoid mismatch effect of rechargeable battery cells when a series-connected stack is formed. The series connection of battery cells is utilized in many applications to boost the output voltage, e.g., EV and bulk storage units for grid support. In one string, all battery cells are charged and discharged at the same level of current, which is prone to potential damage or lifetime reduction if nonuniformity exists among cells. Figure 9.2 illustrates one equalization example using power conversion techniques. Only two battery cells are present to simplify the analysis. When the equivalent circuit is derived and plotted, the conversion topology is related to the buck-boost converter. The metal-oxide semiconductor field-effect transistor (MOSFET), Q2, is used to replace the freewheeling diode in the conventional buck-boost converter. Thus, the bidirectional power flow is activated to exchange energy among the battery cells via the interlinking inductor, L. The on-state duty ratio of Q1 determines the power flow direction and level. Another FET, Q2, is complementarily switched to maintain the inductor current flow. When a 50% duty ratio is applied, the terminal voltage of the two battery cells is theoretically the same according to the steady-state analysis of buck-boost converters. If unbalancing happens, the cell with a higher voltage will be discharged and supply power to the lower-voltage cell until a new equalization is reached. FIGURE 9.2 Bidirectional DC/DC for battery equalization by buck-boost topology. The ´ Ćuk converter shares the same voltage conversion ratio as the buck-boost converter in the steady state. The bidirectional version can also be used to equalize battery cells, as illustrated in Fig. 9.3. The passive switch is replaced with an active switch, MOSFET. The capacitor CSW is utilized as the central interlink for energy exchange and power conversion. In theory, the battery terminal voltage in steady state should be the same when a 50% duty cycle is alternatively applied to the two active switches. FIGURE 9.3 Bidirectional DC/DC for battery equalization using ´ Ćuk topology. The synchronous buck converter is widely applied for ELV power interfaces because of the high efficiency and linear voltage conversion ratio in the continuous conduction mode (CCM). The circuit is illustrated in Fig. 9.4, which is constructed by an active two-switch bridge. When the terminal vhigh is connected to the source, the circuit forms a buck converter that allows power flow from the left to the right, where a load is connected. When the terminal vlow is connected to a source, the topology is changed to a boost converter that can supply active power from right to left. FIGURE 9.4 Non-isolated DC/DC converter formed by two active switches. When both sides include sources and loads, the bidirectional power flow can be achieved since both terminals can perform power sink and source. The duty ratio for PWM determines the direction and level of power flow with regards to the steady-state voltage levels of vhigh and vlow. The condition of the bidirectional power flow is that vlow < vhigh in steady state. When vlow ≥ vhigh, the converter is out of control since the antiparallel diode of QH creates a path for direct current flow. One special bidirectional DC/DC topology draws recent attention, which is the dual active bridge (DAB) DC/DC converter. The topology is not new since it was released in 1989 as a US patent, indexed as 5027264. Thyristors were shown in the patent to construct the active bridges. The latest implementations are based on FETs and IGBTs. The topology is flourishing because of features of bidirectional power flow and galvanic isolation. One discussion is about solid-state transformers, which are expected to replace conventional transformers used in AC electric power distribution. Figure 9.5 demonstrates the transformer function linking a LVAC network with the MVAC grid. The power electronic device reduces the size and weight of power transformation and adds controllability to improve AC power systems. The interlink can be achieved by a DAB to serve the functions of voltage conversion, bidirectional power flow, and galvanic isolation. The features also allow the topology to interface rechargeable battery packs, as discussed at the beginning of the chapter. FIGURE 9.5 Dual active bridge used for the internal link solid-state transformers. Figure 9.6 illustrates the circuit of a DAB converter including two active four-switch bridges, shown as the primary bridge (PB) and the secondary bridge (SB). The interlink between the AC ports are the HF transformer, Tr, and the inductor, L. The diagonal switching devices in each bridge are paired and controlled by the same gate signal for on/off to produce either [+] cycle or [−] cycle. The paired switching scheme of the PB and SB is shown in Tables 9.1 and 9.2, respectively. The two active bridges produce high-frequency AC (HFAC) to exchange power through the interlinking transformer and inductor. FIGURE 9.6 Standard circuit of dual active bridge. TABLE 9.1 Paired Switching Scheme of Primary Bridge TABLE 9.2 Paired Switching Scheme of Secondary Bridge In a steady state, the voltages at the DC terminals are steady, shown as VDCP and VDCS. The two active bridges act as DC/AC conversion to produce HFAC voltage signals, vpb and vsb, as shown in Fig. 9.6. The amplitude difference between vsb and vse comes from the winding turns ratio, n. The amplitudes of vpb and vse can be determined as VDCP and VDCS/n, respectively. The key waveforms are demonstrated in Fig. 9.7 for the steady-state analysis. The modulation of DAB produces the same switching frequency of the signals of vpb, vsb, and vse. The inductor voltage depends on the difference of vpb and vse, which is expressed by vL = vpb − vse. The inductor current responds to the crossing voltage and shows FIGURE 9.7 Waveforms of dual active bridge at steady state in time domain. According to the DAB circuit, as shown in Fig. 9.6, the instantaneous power can be expressed by p(t) = vpb(t) × iL(t). Figure 9.7 indicates the repeated cycle of p(t) from 0 to T2. The averaged value of p(t) indicates the direction of the active power in steady state. If the averaged value is positive, AVG[p(t)] > 0, the active power flow is from the PB to the SB. The time difference between vpb and vse is shown as T1, which is constant in the steady state. Due to the interlinking inductance, L, the inductor current is limited by the switching frequency. Since iL is AC and zero-mean in steady state, the signal shows the repeatable sequence with four states, which are divided by the moments, T1, T2, and T3. Regarding the periodic waveform of iL, as shown in Fig. 9.7, the following condition holds: Considering the time period from 0 to T1, the value of iL changes from iL(0) to iL(T1), which is expressed by where VSE is the amplitude of vse and theoretically equal to Following (9.1), (9.3), and (9.4), the initial value of iL can be determined by Substituting iL(0) in (9.3) yields the expression for iL(T1) in (9.6). The four current levels of iL in the steady state become known since iL(T2) = −iL(0) and iL(T3) = −iL(T1). According to Fig. 9.7, the power waveform is repeated for each half cycle, 0–T2. Therefore, the averaged power can be computed by The averaged value of p(t) in a steady state is determined by In the steady state, the DAB signals are periodic, which can also be translated into the phase representation regarding the switching frequency, ω. The phase angle is normalized by following the reference signal of vpb from 0 to 2π, as shown in Fig. 9.8. The time delay, T1, between vpb and vse, as shown in Fig. 9.7, is then equivalent to the phase shift, ϕ = ωT1. The half-cycle period, T2, is expressed by π in the phase representation. Following (9.8), the average power in steady state can be transformed into the expression in phase format. A nonlinear equation is derived as (9.9), which indicates the control variables ϕ and ω. It shows that the power level goes up by a decrease of ω. When ω is fixed for the switching operation, the phase angle ϕ between vpb and vse becomes the main control input to regulate the power flow. FIGURE 9.8 Waveforms of dual active bridge in phase domain. When 0 < ϕ < π, the averaged power is positive in value by following (9.9). When ω is a constant, the averaged power in steady state is a function of the applied phase, ϕ, which can be expressed by pavg(ϕ). The maximum power level can be determined by the partial differentiation, The highest power flow happens in steady state when the control variable is assigned to be where fsw is the frequency of vpb or vsb in hertz and ω = 2πfsw. Following the above steady-state analysis, the design procedure of a DAB follows: 1. Specify the nominal values of VDCP and VDCS. 2. Specify the power rating or the highest power level, Pmax. 3. Decide the proper winding turns ratio, n, based on the ratio of VDCP and VDCS. 4. Specify the switching frequency, fsw, and ω = 2πfsw. 5. Determine the value of the interlinking inductance, L, according to The analysis in Sec. 9.2.1 shows the averaged power value is positive. Modulation can achieve reverse power flow. An example of the reverse power flow is shown in Fig. 9.9, where the averaged power is computed to be negative in value. Regarding the periodic waveform of iL in each switching moment, as shown in Fig. 9.9, the following condition holds: FIGURE 9.9 Waveforms of dual active bridge showing reverse power flow in time domain. Following Fig. 9.9, the value of iL changes from iL(0) to iL(T1), which is expressed by where VSE is the amplitude of vse and theoretically equal to Following (9.13), (9.15), and (9.16), the initial value of iL can be determined by The value of iL(T2) in steady state is known according to (9.14). When iL(0) is known, by applying (9.3), the current at T1 is derived by (9.18). The current level of iL(T3) becomes known by (9.13). According to Fig. 9.9, the power waveform is repeated for each half cycle, 0–T2. Therefore, the averaged power flow can be computed by following (9.7) and results in Since T21 < T1T2, the averaged power shows a negative sign, which indicates the reverse power flow is from the port of VDCS to VDCP. The periodic signals can be converted into the phase representation, as shown in Fig. 9.10. The phase of vpb is lagging to that of vse or vsb in the representation. The lagging phase is defined as a negative value of ϕ. Therefore, the equivalence is shown as ωT1 = π + ϕ, ωT2 = π, and ωT3 = 2π + ϕ. The averaged power in steady state can be determined by (9.20), where ϕ < 0. FIGURE 9.10 Steady-state waveforms of DAB showing reverse power flow in phase domain. The averaged power computed by (9.20) is negative in value since ϕπ + ϕ2 < 0. When ω is a constant, the averaged power in steady state is a function of the applied phase, ϕ. Applying to (9.20), the critical phase value is determined by (9.21) to represent the maximum level of the reverse power flow. The forward power flow of a DAB is expressed by (9.9) considering According to (9.22), the power flow is controlled by the phase shift ϕ for both directions. The value of ϕ can be modulated to show the phase difference between the AC signals of vpb and vsb. The sign of ϕ indicates either the leading or lagging between vpb and vse and the power flow direction. Figure 9.11 shows the conversion plot between the delivered power and the phase angle, ϕ. The maximum flow volume is achieved for both directions when |ϕ| = π/2. The switching frequency can be used as an additional control variable for power flow regulation, as indicated in Fig. 9.11. FIGURE 9.11 Averaging power versus phase angle in DAB. The above steady-state analysis is based on one condition that VDCS/n > VDCP, which is shown in Figs. 9.7 and 9.9. It should be noted that many cases show VDCS/n ≤ VDCP. However, the averaged power is computed using (9.22). Figure 9.12 illustrates the phase representation, in which the active switching happens at ϕ, π , ϕ + π, and 0. One pair of active switches are turned off at the switching moment, meanwhile, another pair is switched on for conduction. A short dead time should be applied in between to prevent shoot through. Figure 9.12 also indicates the predefined four states for analysis, which are divided by the switching moments. FIGURE 9.12 Key waveforms to define the switching moments and operational states. Consider the inductor current from phase 0 to phase ϕ; there is a zero-crossing point under state 1, as shown in Fig. 9.12. The inductor current changes from the negative to positive value. The corresponding status of the eight switches is demonstrated in Fig. 9.13a,b, for the periods when iL < 0 and iL > 0, respectively. The switching action happens at the moment ϕ. The pairs of the SB, QSBH and QSAL, are switched off. The transition can be checked by the difference between Figs. 9.13b and 9.14. A short dead time should be applied before the gate signals sent to the opposite pairs. During the dead time, the antiparallel diodes of QPAH and QPBL are forward-biased to keep iL flow in the same direction. When gate signals are applied to turn on the pair of QSAH and QSBL, the zero-voltage switching (ZVS) is realized because of the conduction of the antiparallel diodes, which clamps the crossing voltage to zero. FIGURE 9.13 Circuit status of operation state 1: (a) iL < 0; (b) iL > 0. Figure 9.14 demonstrates the circuit status at state 2, between the phase of ϕ to π, as indicated in Fig. 9.12. Active switching happens on PB at π to make the transition from state 2 to 3. The pairs of the PB, QPAH and QPBL, are switched off. During the dead time, the antiparallel diodes of QPBH and QPAL are forward-biased to keep iL flow in the same direction. The ZVS is realized for the turning-on because of the pre-conduction of the anti-parallel diodes, as shown in the transition from Fig. 9.14 to 9.15a. A zero crossing of iL happens within state 3, in which the inductor current changes from positive to negative, as shown in Fig. 9.12. The substate circuits are illustrated in Fig. 9.15a,b showing the current flow difference. FIGURE 9.14 Circuit status of operation state 2. FIGURE 9.15 Circuit illustration of operation state 3: (a) iL > 0; (b) iL < 0. A transition happens at the moment of π + ϕ, as indicated in Fig. 9.12. The pairs of the SB, QSAH and QSBL, are switched off. The transition is shown by comparing Fig. 9.15b with Fig. 9.16. During the dead time, the antiparallel diodes of QSBH and QSAL are forward-biased to keep iL flow in the same direction, which leads to ZVS for turning on QSBH and QSAL. The fourth state is maintained from π + ϕ to 2π, as illustrated in Figs. 9.12 and 9.16. A new transition happens at the end of state 4. The switching can be referred to as the initial point in phase, as shown in Fig. 9.12. The pairs of the PB, QPBH and QPAL, are switched off. During the dead time, the antiparallel diodes of QPAH and QPBL are forward-biased to keep iL flow in the same direction, which leads to ZVS for turning on QPAH and QPBL. It is shown in the transition from Fig. 9.16 to Fig. 9.13a. FIGURE 9.16 Circuit illustration of operation state 4. The above analysis is based on the the forward power flow, as shown in Fig. 9.12. Table 9.3 summarizes the operational states regarding the phase, state, current, voltage, power, and equivalent circuits. The analysis shows that the switching-on realizes the ZVS of all switches. The above analysis shows that the current direction of iL at the switching moment is critical to realize ZVS. The current flow should lead the antiparallel diode forward-biased before the gate signals and support the turning on with ZVS. Based on the above analysis, Table 9.4 summarizes the condition for the switching-on with ZVS. The ZVS is supported by the direction of the inductor current at the switching moment. The summary is general for all case study of ZVS realization for DABs. TABLE 9.3 Operational States of Full-Scale ZVS of Forward Power Flow TABLE 9.4 Condition of ZVS for Switching On Figure 9.17 illustrates the steady-state waveforms representing the reverse power flow. The operational states are defined that are based on the four switching moments. According to the steady-state waveforms in Fig. 9.10, the operational states of reverse power flow are defined and summarized in Table 9.5, which lists the four states and their status in terms of phase, current, voltage, and power. The full-scale ZVS is also satisfied for the turn-on operation of the active switches, which agrees with the conditions defined in Table 9.4. FIGURE 9.17 Key waveforms to define switching moments and operational states when power flows reversely. The zero crossings of iL should happen in the correct states to satisfy the conditions listed in Table 9.4. One condition can always ensure the correct switching sequence for the ZVS, which is expressed by FIGURE 9.18 Waveforms of forward power flow under the flattop condition. FIGURE 9.19 Waveforms of reverse power flow under the flattop condition. TABLE 9.5 Operational States for Full-Scale ZVS of Reverse Power Flow Most DABs cannot always maintain the flattop condition due to variation of the DC terminal voltages. Figure 9.20 illustrates one case of the forward power flow that the amplitude of vpb is lower than that of vse. Due to the low value of ϕ, the two zero crossings of iL happen in the states 2 and 4 instead of in states 1 and 3, which is shown in Fig. 9.12 and described in Table 9.3. The switching-on of QPBH and QPAL loses the ZVS since iL < 0 at π, which is opposite to the condition defined in Table 9.4. The ZVS of QPAH and QPBL is also lost since iL > 0 at the switching-on moment. Thus, the four switches of the PB cannot realize ZVS during turn-on at 0 and π. The direction of iL is correct for the ZVS of the four switches in SB, as shown in Fig. 9.20. FIGURE 9.20 Waveform indicating partial loss of ZVS in case of Figure 9.21 demonstrates another case of the forward power flow that the amplitude of vpb is higher than that of vse. Due to the low value of ϕ, the two zero crossings also happen in states 2 and 4 instead of in states 1 and 3. The ZVS for turning on QSAH and QSBL is lost since iL < 0 at ϕ. The ZVS of QSBH and QSAL is also lost since iL > 0 at the switching moment. The four switches of the SB fail to realize ZVS during turn-on at ϕ and π + ϕ. The direction of iL is correct for the ZVS switching-on of the four switches in PB, as shown in Fig. 9.21. The loss of ZVS is caused by the voltage difference and low level of phase shift between vpb and vse. FIGURE 9.21 Waveform indicating partial loss of ZVS in case of Figure 9.20 indicates an early zero crossing of iL that happens in states 2 and 4 instead of in states 1 and 3 due to The steady-state waveforms at the critical condition (ϕ = ϕcrit) are shown in Fig. 9.22 in the case of forward power flow and FIGURE 9.22 Waveforms of forward power flow in case of FIGURE 9.23 Waveforms of forward power flow in case of VSE < VPB and ϕ = ϕcrit. Figure 9.23 illustrates the steady-state waveforms in the case of the forward power flow that the amplitude of vpb is higher than that of vse. The critical condition (ϕ = ϕcrit) shows that the switching moment of the SB happens at iL = 0. The switching-on of the SB switches can achieve both ZVS and ZCS. The instantaneous power enters the negative zone, indicating power circulation. A general equation can be derived to represent the critical phase shift angle for the forward power flow, as expressed in (9.25). It is derived from the two different cases and expressed in both (9.23) and (9.24). Regarding nVDCP ≠ = VDCS, a non-zero ϕcrit is determined. When |ϕ| ≥ |ϕcrit|, the switching sequence is correctly maintained for the ZVS of all eight switches. For nVDCP = VDCS, the evaluation shows ϕcrit = 0, which indicates the flattop of iL and no constraint for the ZVS. In the case of reverse power flow, the derivation of the critical phase angle shows the same as (9.25). In summary, the full-scale ZVS is achieved when the condition is maintained by |ϕ| ≥ ϕcrit, for either the forward or reverse power flow status. A Simulink model can be constructed according to the operational principle of DAB, as illustrated in Fig. 9.24. The model of DAB requires the voltage levels of VDCP, VDCS, and the switching control signals for all active switches, as shown in Fig. 9.24a. The variation of VDCP and VDCS depends on the profiles of sources and loads at the DC terminals. The output signals include the two voltage levels across the inductor, vpb and vse, and the inductor current, iL. The gate signals of “PWM-PA” and “PWM-SA” can be generated to indicate the phase difference. Another two PWM signals for leg B are the complementary signals for leg A. The block for phase-shift modulation, as shown in Fig. 9.24b, can be built, which has been introduced in Sec. 5.4.2. The modulation should produce pulses for the signals of “PWM-PA” and “PWM-SA,” which show the phase shift. FIGURE 9.24 Simulink model of (a) dual active bridge; (b) integrated with modulation. TABLE 9.6 Design Requirement of Dual Active Bridge A case study is based on the specification in Table 9.6. According to (9.12), the interlinking inductor can be sized to show L = 1.9 μH. Following (9.25), the critical phase shift can be identified as ϕcrit = 0.38 rad or 22°, which shows the boundary of the full-scale ZVS. Figure 9.25 shows the simulation result that the reverse power flow is modulated by ϕ = −0.38 rad. According to (9.22), the averaged power is −426 W, which is verified by the simulation result. The circuit with this set of parameters can produce power flow ranging from −1 kW to 1 kW, which is regulated by the phase shift from FIGURE 9.25 Simulated waveforms of DAB showing phase shift ϕ = ϕcrit. Modern power systems tend to more and more distributed power generation interfaced by power converters. Lack of system inertia is becoming a major concern since the traditional power generation is based on electric machines. The turbine-based generator shows significant stored energy in the rotating masses, which can be used to support grid stability. The alternative solution to maintaining grid stability is the increasing installation of energy storage, e.g., rechargeable batteries and ultracapacitors. The bidirectional power conversion between DC and AC is demanded to interface such DC devices. For small-scale applications, the power conversion is commonly between DC and single-phase AC. The power interface between DC and three-phase AC is required for large-scale power applications. Chapter 5 discussed the power conversion from DC to single-phase AC. Figure 5.3 shows the typical bridge circuits to perform the conversion. The DC/AC voltage conversion can only achieve a step-down operation since the RMS value of vab in steady state is less than the DC input voltage, Vin. Thus, a fully controlled DC/AC operation is based on the DC voltage, which is always higher than the peak of vab in steady state. Following the bridge, as shown in Fig. 5.3, the AC/DC conversion can be automatically realized when the instantaneous value of vab is higher than Vin due to the presence of the antiparallel diodes. The power conversion from the single-phase AC to DC depends on the forward-biased status of the diodes, which is out of control. Whenever vab(t) > Vin, a pair of diodes automatically conduct to transfer power from the AC side to the DC terminal, regardless of the condition of active switches. Thus, the bridges designed for DC to single-phase AC conversion are capable of performing bidirectional power conversion but constrained by the voltage difference of the AC and DC sides. Figure 8.3 illustrates the typical bridge circuit to achieve power conversion from DC to three-phase AC. A fully controlled DC/AC operation is based on the condition that the DC voltage, vin, is always higher than the amplitude of AC voltage. On the other hand, power conversion can happen from the three-phase AC to DC due to the antiparallel diodes, as shown in the bridge circuit. The power conversion from the three-phase AC to DC depends on the forward-biased status of the six diodes. Whenever any LL voltage of the three-phase AC side is higher than the DC level, Vin, a pair of diodes conducts to transfer power from AC to DC. In principle, the bridges designed for DC to three-phase AC conversion are capable of performing bidirectional power conversion but constrained by the voltage levels of the AC and DC sides. For many applications of three-phase AC drives, such as EVs, cranes, or elevators, the motor can also perform as an alternator or a generator. The electric power generation happens when mechanical force pulls the rotation faster than its synchronous speed. Traditionally, the kinetic energy is converted to joule heat wasted and dissipated by braking resistors in order to maintain the voltage stability. Such a solution has been discussed at the beginning of Chap. 8. Figure 8.2 shows the system circuit indicating the braking resistor, RB, and the chopping switch, QB. The diode bridge is incapable of performing DC/AC conversion to recycle energy back to the AC grid. Energy should not be wasted but recycled or deposited to either grid or energy storage. Bidirectional AC/DC conversion is required for the variable frequency drive system to recover regenerating energy. The latest solution presents the back-to-back active bridges, which are shown in Fig. 9.26. Regulating the DC link voltage can control bidirectional power flow between the source and the motor. The nominal power flow is from the AC source to the motor via the AC/DC, DC link, and DC/AC. When the motor starts power generation, the DC-link voltage will increase until the level that energy can be extracted and injected into the grid. Therefore, the two active bridges show the capability of bidirectional power flow, recycle regeneration power from the motor, and eventually improve the system efficiency. FIGURE 9.26 Variable frequency drive for motors with bidirectional DC/AC conversion. The synchronous switching of non-isolated DC/DC converters shows the capability of bidirectional power conversion. The freewheeling diode in such converters should be replaced by a FET to achieve the bidirectional power flow. The buck-boost and Ćuk topologies demonstrate the controllable conversion for both directions. Therefore, the converters are commonly used for battery cell equalization. The synchronous buck converter is equivalent to a boost converter, depending on the configuration of input and output. It supports bidirectional power flow but shows the constraint of the terminal voltages. The steady-state analysis of the above non-isolated topologies is based on the voltage conversion. Lately, the DAB is used for bidirectional power conversion because of the features of controllable power flow, galvanic isolation, and soft switching. The advances in power semiconductors make the topology more cost-effective and efficient than before. The technology of phase shift is typical to regulate the power flow in either direction. Variation in switching frequency can also be added to control the level of power flow. The design challenge of DAB lies in maintaining high conversion efficiency to cover a broad range of load conditions. The topology mostly shows circulating power in steady state when the regular phase-shift method is used for modulation. It is known that circulating power increases the conduction loss in the circuit. Low levels of phase shift can reduce power conversion levels but result in the loss of soft switching and increasing weight of circulating power. Thus, tremendous research focuses on advanced modulation technology to enhance the soft-switching range and minimize the circulating power to improve conversion efficiency. The active four-switch and six-switch bridges can support the bidirectional power flow. The topologies are commonly designed to support the step-down voltage conversion from DC to AC. Therefore, the DC/AC conversion is controllable when the DC side shows a higher voltage level than the AC side. Otherwise, the antiparallel diodes in the bridge form a rectifier to convert AC to DC automatically. The feature can be used to convert regeneration power from a rotating motor and recycle the energy. 1. R. W. DeDoncker, M. H. Kheraluwala, and D. M. Divan, Power conversion apparatus for DC/DC conversion using dual active bridges, US patent, #US5027264A, 1991. 2. I. Syed, W. Xiao, and P. Zhang, “Modeling and affine parameterization for dual active bridge DC-DC converters,” Electric Power Components and Systems, Vol. 43, No. 6, pp. 665–673, 2015. 3. H. Wen, B. Su, and W. Xiao, “Design and performance evaluation of a bidirectional isolated DC–DC converter with extended dual-phase-shift scheme,” IET Power Electronics, Vol. 6, no. 5, pp. 914–924, May 2013. 4. H. Wen, W. Xiao, and B. Su, “Nonactive power losses minimization in a bidirectional isolated DC-DC converter for distributed power system,” IEEE Transactions on Industrial Electronics, Vol. 61, no. 12, pp. 6822–6831, 2014. 5. Yuang-Shung Lee and Ming-Wang Cheng, “Intelligent control battery equalization for series connected lithium-ion battery strings,” IEEE Transactions on Industrial Electronics, Vol. 52, no. 5, pp. 1297–1307, October 2005. doi: 10.1109/TIE.2005.855673. 6. N. H. Kukut, A modular nondissipative current diverter for EV battery charge equalization, Applied Power Electronics Conference and Exposition, 1998. 7. H. Wen and W. Xiao, “Bidirectional dual-active-bridge DC-DC converter with triple-phase-shift control,” in Proceedings of IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, 2013, pp. 1972–1978. 8. M. Farhangi, W. Xiao, and H. Wen, “Advanced modulation scheme of dual active bridge for high conversion efficiency,” IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, 2019, pp. 1867–1871. 9.1 Follow Sec. 9.2.6 and build your own simulation model for DAB. 9.2 Based on the DAB specification in Table 9.6, perform the following simulation under the condition of • • ϕ = ϕcrit and ϕ = −ϕcrit. • when ϕ = 0.2 rad, compute the averaged value of power, get the simulation result, and discuss the ZVS realization of switching-on operation. 9.3 Based on the DAB specification in Table 9.6, the winding turns ratio is changed from 1:6 to 1:10. Other parameters remain the same. (a) Compute the L value to satisfy the specification. (b) Simulate the circuit based on (c) Find the new value of ϕcrit and simulate the DAB with ϕ = ϕcrit and ϕ = −ϕcrit. (d) When ϕ = −0.2 rad, compute the averaged value of power, get the simulation result, and discuss the ZVS realization of switching-on operation. 9.4 Based on the DAB specification in Table 9.6, the winding turns ratio is changed from 1:6 to 1:7.92. Other parameters remain the same. Compute the L value to satisfy the specification, simulate the circuit based on ϕ = 0.2 rad, and discuss the ZVS realization of switching-on operation.
CHAPTER9
Bidirectional Power Conversion
9.1 Non-Isolated DC/DC Conversion
9.2 Dual Active Bridge
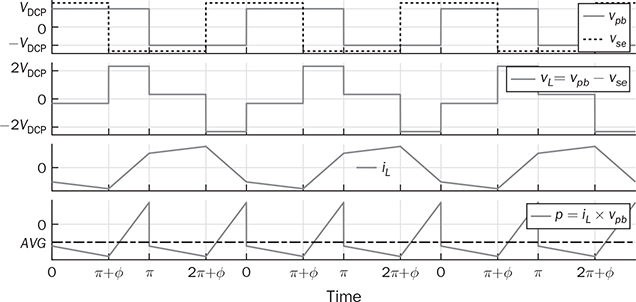
9.2.1 Forward Power Flow
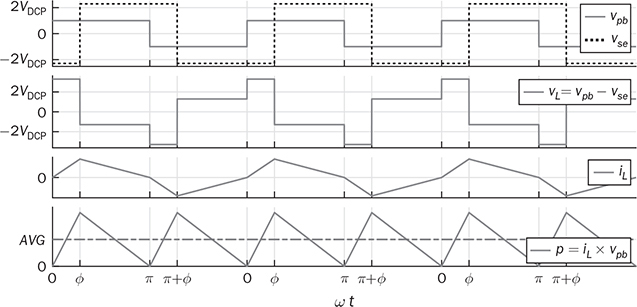
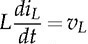. The instantaneous level of nonzero vL leads to the amplitude of iL increasing or decreasing, as illustrated in Fig. 9.7. The signal of iL is AC and indicates the zero mean in each steady-state cycle.
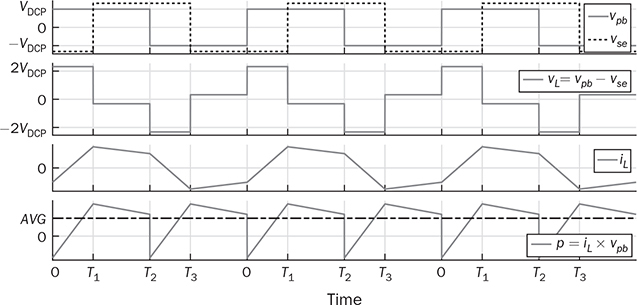
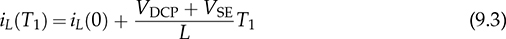
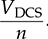. From T1 to T2, the inductor current reaches to the new level:
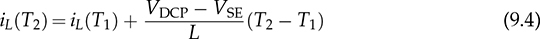
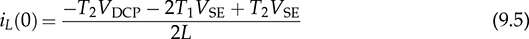
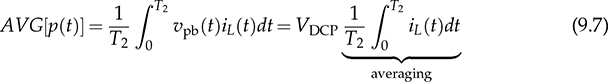
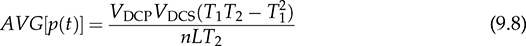
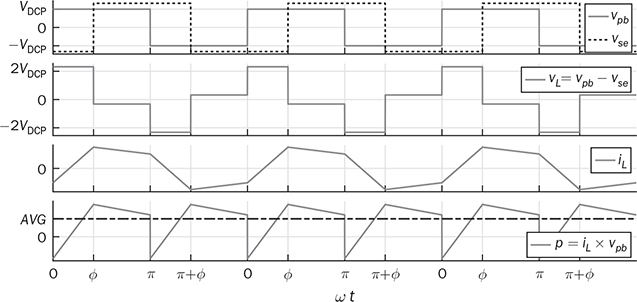
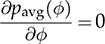. Following (9.9), the critical phase value that represents the highest power flow is determined by
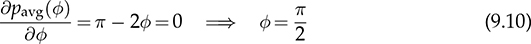
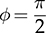. The highest value of the averaged power is expressed by (9.11) to represent the power rating.
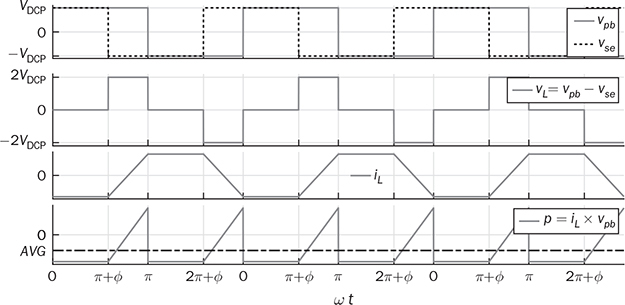
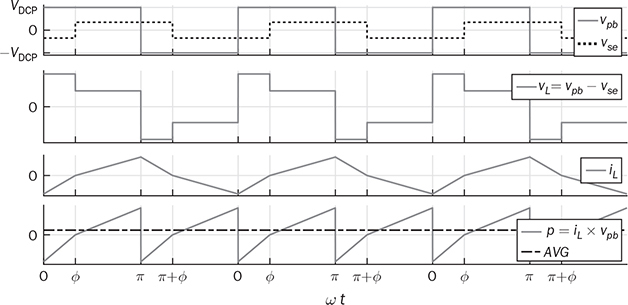
9.2.2 Reverse Power Flow
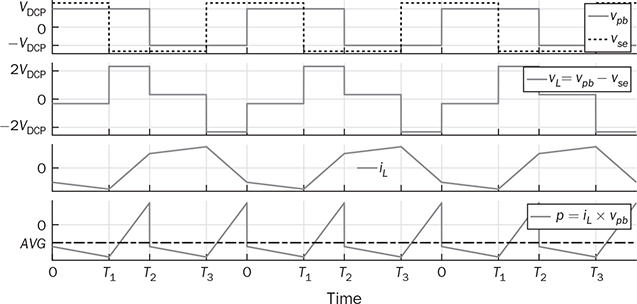
. From T1 to T2, the inductor current reaches to the new level
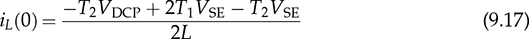
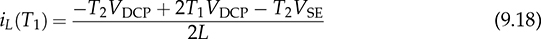
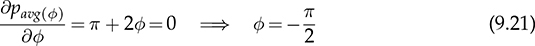
while, the reverse power flow is shown by (9.20), considering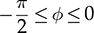 
. A universal expression for the averaged power can be derived as
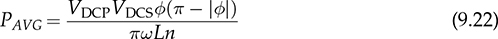
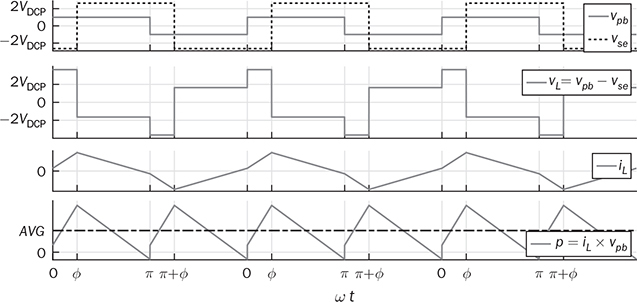
9.2.3 Zero-Voltage Switching
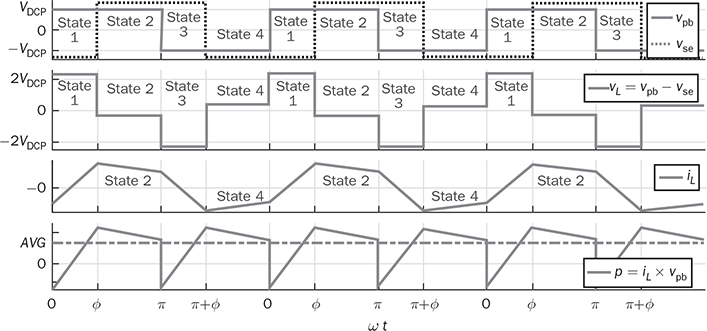
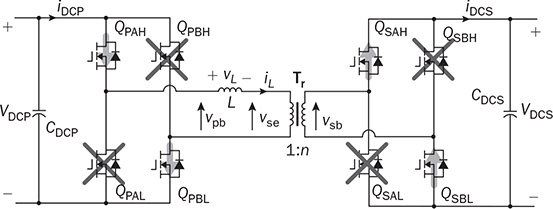
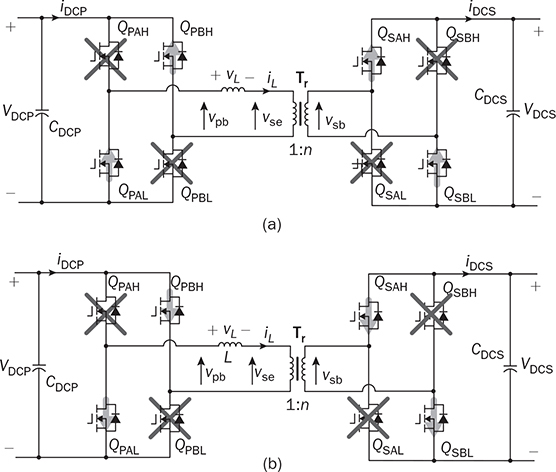
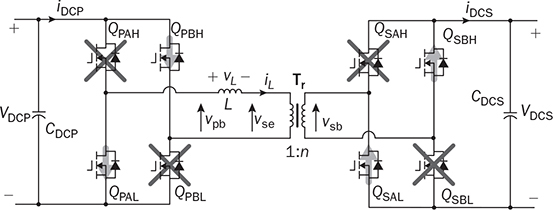
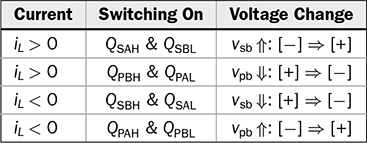
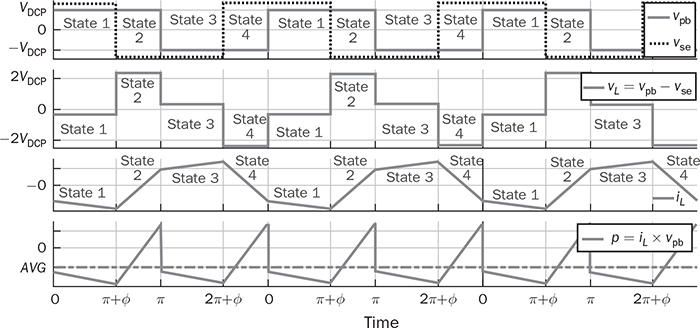
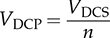. The condition results in the equal amplitude of vpb and vse. Figure 9.18 illustrates the steady-state waveforms to show the “flattop” of iL when the forward power flow is modulated by a positive value of ϕ. The cancellation leads to vL = 0 and the flattop of iL. The steady-state condition of the reverse power flow is shown in Fig. 9.19, where 
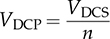. The flattop condition in steady state guarantees that the iL direction always supports ZVS for switching on, which is described in Table 9.4.
9.2.4 Losing Zero-Voltage Switching
.
.
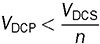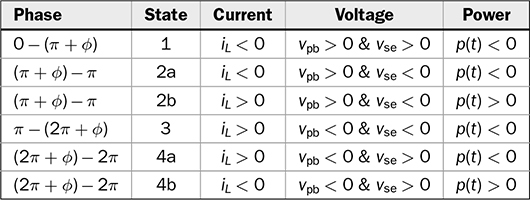
9.2.5 Critical Phase Shift for ZVS
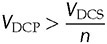. The mismatch is caused by the amplitude difference of vpb and vse, and the low value of ϕ. A constraint can be defined to maintain the ZVS of all switches in case that the amplitude of vpb is less than vse. The condition is that ϕ should be significant to make iL(0) ≤ 0. Thus, the boundary is iL(0) = 0, which leads to derivation of the critical value of ϕ. Following (9.5), the critical value of phase shift is derived in (9.23). When ϕ ≥ ϕcrit, the switching sequence is correctly maintained to switch on all eight switches with ZVS, in case of the forwarding power flow and 
.
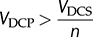. The switching moment of the switches in the PB happens at iL = 0, which indicates the realization of both ZVS and ZCS. It is also interesting that the power circulation is rejected under the operating condition since the instantaneous value of p(t) is above zero in the steady state. Figure 9.21 shows a late zero crossing of iL that happens in states 2 and 4 instead of in states 1 and 3 
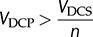. To maintain the ZVS of all switches in the SB, the ϕ should be within the range in order to satisfy iL(ϕ) ≥ 0. The boundary becomes iL(ϕ) = 0. Following (9.6), the critical value of phase shift is derived in
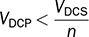and ϕ = ϕcrit.
9.2.6 Simulation and Case Study
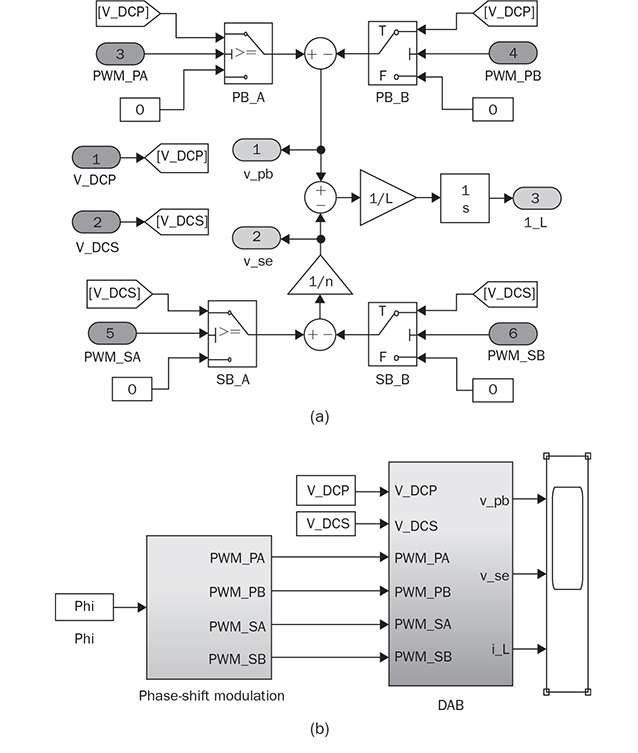
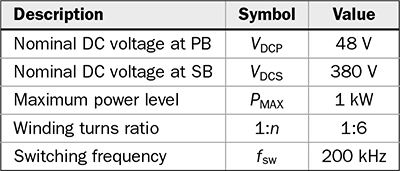
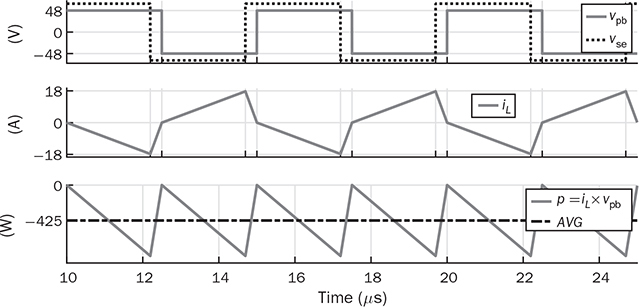
,respectively.
9.3 Conversion Between DC and AC
9.3.1 Between DC and Single-Phase AC
9.3.2 Between DC and Three-Phase AC
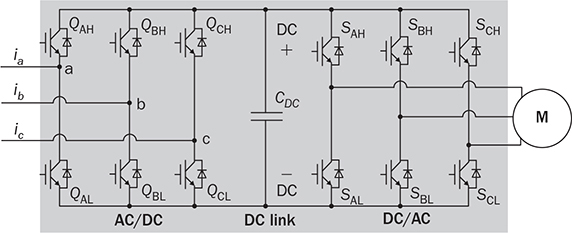
9.4 Summary
Bibliography
Problems
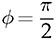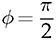and 
.
and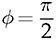 
.