Abstract
The estimation analysis method or more commonly referred to in everyday use as hand calcualtions is described here, where a systematic approach including a “feedback” loop to ensure correctness of model is used.
1.1 Introduction
This chapter provides a summary of steps needed to make useful mathematical models of physical systems. I refer to these steps as “estimation analysis” but in hallways of science and engineering schools or engineering offices they are often referred to as hand calculations or back-of-the-envelope calculations. I am not a big fan of these terms, as they convey a sense of sloppiness, which is far from accurate. This type of analysis is useful for building deeper understanding of integrated circuits and systems, but the methodology is very general and can be applied to most systems governed by some kind of mathematics. From deep space astrophysics to microscopic systems such as integrated circuits you will find broad applications of this kind of thinking. With this broad applicability it is no surprise that the principles we outline here are somewhat vague, but we will discuss enough examples in the rest of the book to enable the reader to develop a good sense of how to proceed in different situations. A mastery of these ideas will only come with experience. The process can be time-consuming initially because it involves digging into the core of the system under consideration. If the system is new to the user, the learning process can take even longer. But oftentimes, and with practice, the systems are similar enough to other systems the user has seen before that the process can be quite swift. We will start by outlining the principles and then discuss each of them in some depth. We will then refer to these steps in the following chapters, where many examples are provided.
After a model has been developed one can use it as a starting point for fine-tuning in a simulator or on the bench or whatever might be practical.
1.2 Principles
A beginner often tries to solve a problem with brute force, using three dimensions, full nonlinear equations, etc. The problem will then quickly become intractable with myriads of sums and complex expressions yielding little insight. With experience one learns that the core behavior is often much simpler to catch but it requires thinking the problem through before full calculations start. For the novice this can often be frustrating but with practice one learns to see the value of this approach.
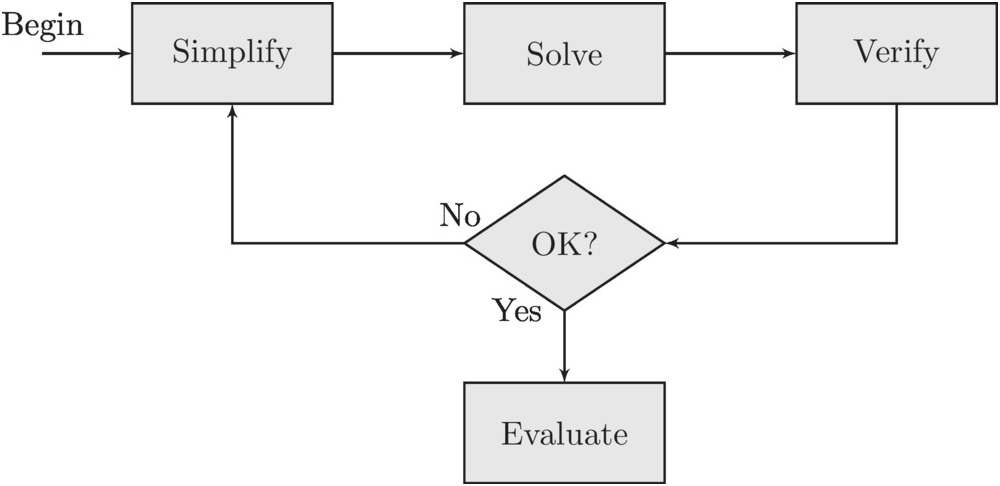
In a typical modeling situation there are four steps to follow:
(1) Simplify – This is often the most difficult step because it attempts to get to the core of how the system works.
(2) Solve – If step 1 is executed properly this will be relatively easy.
(3) Verify – Here we verify the solution in step 2 is correct by for example checking extreme cases and/or comparing to simulations and/or exact calculations. If something is wrong, go back to step 1.
(4) Evaluate – In this section we analyze what the solution means.
We will discuss each of these in turn: see Figure 1.1 for a simple flow diagram.
