6.1 INTRODUCTION

The significance of studying the deformation behavior of components of complex structures in the form of bars, plates, cylinder, disc etc. is not only essential for the basic understanding of mechanical phenomenon but also to build reliable structures. Advances in the field are targeted to assure safety, reliability, and economy in the design of structure and complete systems, hence to the continued development in design of turbines, aerospace and surface transportation vehicles, prosthetics, material processing, and several other manufacturing technologies. The design engineer is interested in deformation behaviors in connection with his responsibility for avoiding excessive deflection or distortion in machine parts and engineering structures. The mechanical properties of the materials have to be considered for the various parts, thereby optimizing the available resources. The designer is also concerned with identification of the limiting condition of stress which further leads to fracture. Hence, necessary deformation rates have to be analyzed. He may base his calculation as far as they refer to pure elastic deformation upon the theory of elasticity, but he lacks in scope when the plastic state sets in. Therefore, the theory of plasticity is made necessary by demand for better design and more economic use of materials as well as for better control of metal working operations such as wire-drawing and cold rolling. Components such as a disc, cylinder, and a spherical shell will be considered in this chapter and the work done by various researchers will be analyzed to provide insights into the reliability of the structural components.

6.2 STRUCTURAL COMPONENTS IN THE FORM OF DISCS, CYLINDERS, AND SHELLS

Rotating disc play an importance role in machine design. The problems of rotating discs were first treated in the early nineteenth century. Solution of the isotropic discs including variable thickness, variable density, and other case can be found in most of the standard elasticity textbooks [1, 2]. Rotating discs were considered to be one of the exhausted subjects in the field of solid mechanics. Recently new interests have been generated to reinvestigate these problems. The new interest is the result of the development of composite materials and their applications. Composite materials are characterized by high strength to weight ratios, heterogeneity, and anisotropy characteristics. The analytic method has proved to be a simple and reliable means of generating a biaxial state of stress when the loads cannot be directly applied to the material under investigation. In this case, an analytical solution of this problem is needed to interpret the experimental results generated in the laboratory. Because of the steady increase in the use of energy and the impact of that use on the environment, a flywheel made of composite materials has been proved to be an efficient mean of storing energy. Likewise, analytical solution of rotating discs made of composite materials is essential in design and analysis. The calculation of turbine disc involves the solution of second order differential equation having the elastic stress function. This equation is integrable analytically for discs of constant thickness, and for specific examples of discs of non-constant thickness. Arrowsmith [1] has given solutions for discs whose thickness is inversely proportional to radius to the power thickness parameter while Malkin [3] discusses a disc with exponential thickness variation.

A cylinder is a commonly used component in various structural components. In most of the applications, such as pressure vessel for industrial gases, transportation of high-pressurized fluids and piping of nuclear reactors, the cylinder has to operate under severe mechanical and thermal loads, resulting in significant creep and thereby decreasing its service life. Rimrott [4] has solved the problem of thick-walled isotropic cylinders subjected to internal pressure using finite strain theory and has shown that by considering finite strains the creep rate of a thick walled cylinder subject to internal pressure increases even though the creep rate of the same material when subjected to constant true stress in simple tension is constant.

Love [5] studied vibrations and deformation in thin elastic shells. He assumed small deflections and for that, reason neglected all the higher terms of the quadratic in the energy equation. Thus, he obtained linear differential equations for the determination of the equilibrium position of shell under given forces. The buckling of cylindrical shells of uniform thickness under the action of uniformly distributed axial load was further studied but this was till then only confined to monolithic materials. In the design of shells made of functionally graded materials (FGMs) and homogeneous-isotropic materials, it is of technical importance to examine its resistance to bend under expected loading conditions. For that purpose, the determination of the bending load alone is not sufficient in general, but it is further required to clarify the post bending behavior, that is, the behavior of the shell after passing through the buckling load. Firstly, it is necessary to estimate the effect of practically unavoidable imperfections on the buckling load and the second is to evaluate the ultimate strength to exploit the load-carrying capacity of the shell structure. Von Kârmân and Tsien [6] argued at the time, geometrical nonlinearity must play an important part in the phenomenon of thin shell deformation. Donnell and Wan [7] reported that the initial geometric imperfection has a significant effect on the buckling and post buckling behavior of cylindrical shells subjected to axial compression. In their analysis, however, the membrane pre-buckling state was assumed, like von Kârmân and Tsien [6] did and, therefore, the boundary conditions cannot be incorporated accurately.

Wahl [8, 9] considered a flat disc forged from chromium steel and analyzed it for steady state creep at 538(C. The experimental results for this system were examined theoretically using Tresca and von Mises yield criterion. It is seen that the creep deformations calculated using Tresca criterion provide a better agreement with experimental observations. The results obtained from von Mises criteria are too low in comparison to experimental results, which may be due to the anisotropy of the material used. Author further extended his study to analyze secondary creep in a disc of variable thickness in which he concluded that such a disc had lower difference in maximum and average stress levels as compared to a disc with constant radius.

Rimrott [4] assumed a cylinder made of homogeneous isotropic material with large strain rates and used generally accepted assumptions of constant density, zero axial strain and distortion energy theory and derived equations of creep in a thick walled, closed end, hollow circular cylinder subject to internal pressure considering finite strains, the creep rates increase however the creep rate in the same material subjected to constant true stress in simple tension is constant. Author concluded that thick walled cylinder is an unsafe assumption.

Baker [10] developed a theory for the elastic-plastic response of a thin spherical shell to spherically symmetric internal pressure loading. Analytic solutions were obtained to the linear, small-deflection equations of motion for shell materials which exhibited various degrees of strain-hardening. Numerical solutions obtained by digital computer were also presented for the equations for large deflections obtained by accounting for shell thinning and increase in radius during deformation. The results of this theory are justified by the experimental results.

Ma [11, 12] introduced the parameter of thermal gradient on rotating discs. The analysis was based on the theory of Tresca’s yielding criterion and its associated flow rule while the steady state condition was described by power law. The study revealed that the proposed analysis can be used to obtain closed form solutions for creep stresses.

Seth [13] specified that the usage of classical theory of deformation in the transition stage is totally insufficient as it relies on linearity of the stage. Author defined a transition theory which dealt with the non linear character of the deformation and gave a generalized strain measure to study deformation behavior for different kinds of materials under compression. Author argued that the differential system attains some sort of criticality at transition. These critical or transition points can be predicted giving us asymptotic solutions. Author also stated that at the Elastic-plastic deformation stage, the amount of plasticity will rely on geometry of deformation and not on the stresses.

Hulsarkar [14, 40] applied Seth’s transition theory of elastic-plastic and creep deformations to solve the problem of creep in composite cylinders subjected to uniform internal pressure and rotating discs with steady state temperature. The generalized expressions for creep transition stresses were obtained, which, in a special case reduces to those derived by assuming the creep laws.

Gupta and Shukla [15] obtained elastics-plastic and transitional stresses in a disc with variable thickness subjected to internal pressure using Seth’s transition theory. Non-homogeneity in the disc was due to variation of Poisson’s ratio of the material. It was found that the presence of non-homogeneity and thickness variation influence significantly the stresses and pressure required for initial yielding. The thickness variation reduces the magnitude of the stresses and pressure needed for fully-plastic state.

Loghman and Wahab [16] developed a model to estimate creep damages in a thick-walled tube subjected to internal pressure and thermal gradient. The study predicted the changes in creep damage rates during life cycle of the tube due to variation in stresses with time and through-thickness variations. The θ projection concept was used to predict the long-term creep properties up to rupture and the creep rupture data (Figure 6.1).

Güven [17–19] analyzed fully plastic rotating disc and a hyperbolic annular disc with a rigid shaft attached at the bore. The plane state of stress in these conditions has been considered. Exact solutions are obtained using Tresca yielding criterion. The numerical results indicate that maximum stresses and the plastic flow are influenced by the thickness parameter (Figure 6.2).

Singh and Ray [20] first introduced creep analysis in an isotropic functionally graded material rotating disc of Al-SiCp composite. They investigated the creep analysis in an isotropic FGMs rotating disc made of a composite containing silicon carbide particles (SiCp) in a matrix of pure aluminum at uniform elevated temperature by using Norton’s power law and they assumed the particle distribution is linearly decreasing from the inner to the outer radius along the radial distance in the disc estimated by regression t of the available experimental data. It is observed that the steady state creep response of the functionally graded material disc in terms of strain rates is significantly superior as compared to a similar disk having uniform distribution of SiCp (Figure 6.3).

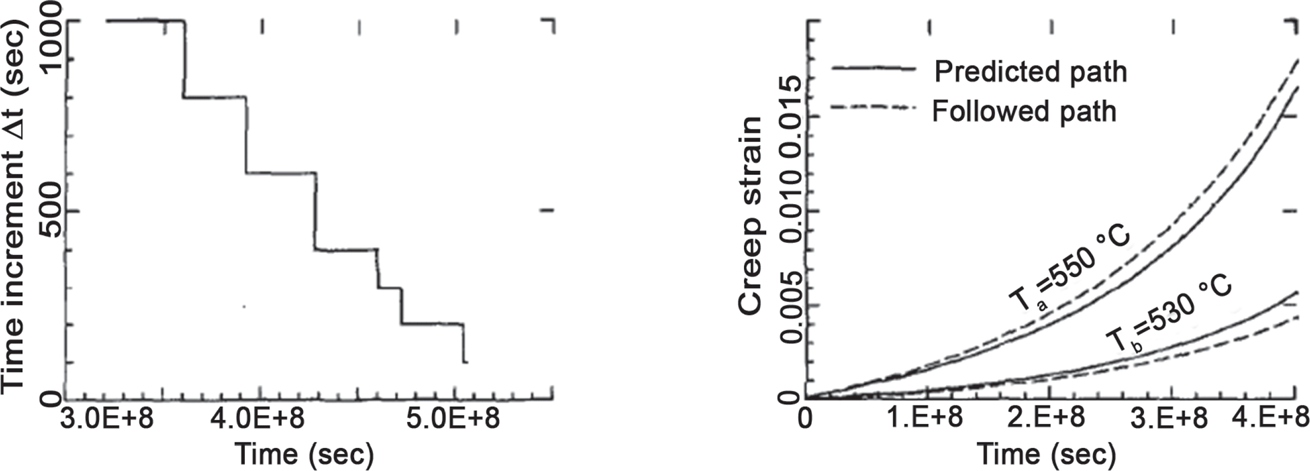
FIGURE 6.1 The time increment variation and predicted path of creep strain [16].

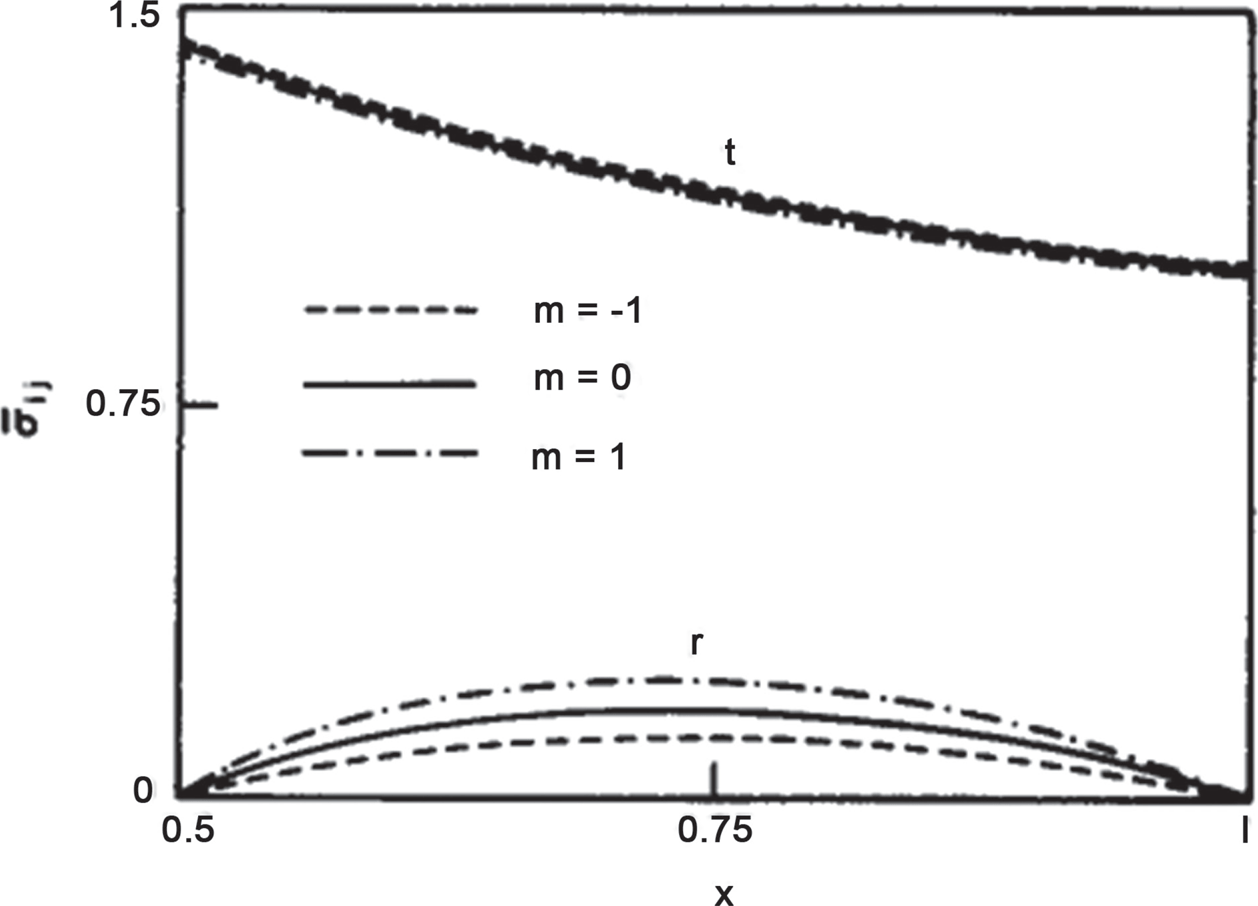
FIGURE 6.2 Stress distribution at fully plastic state with m as thickness parameter [17].

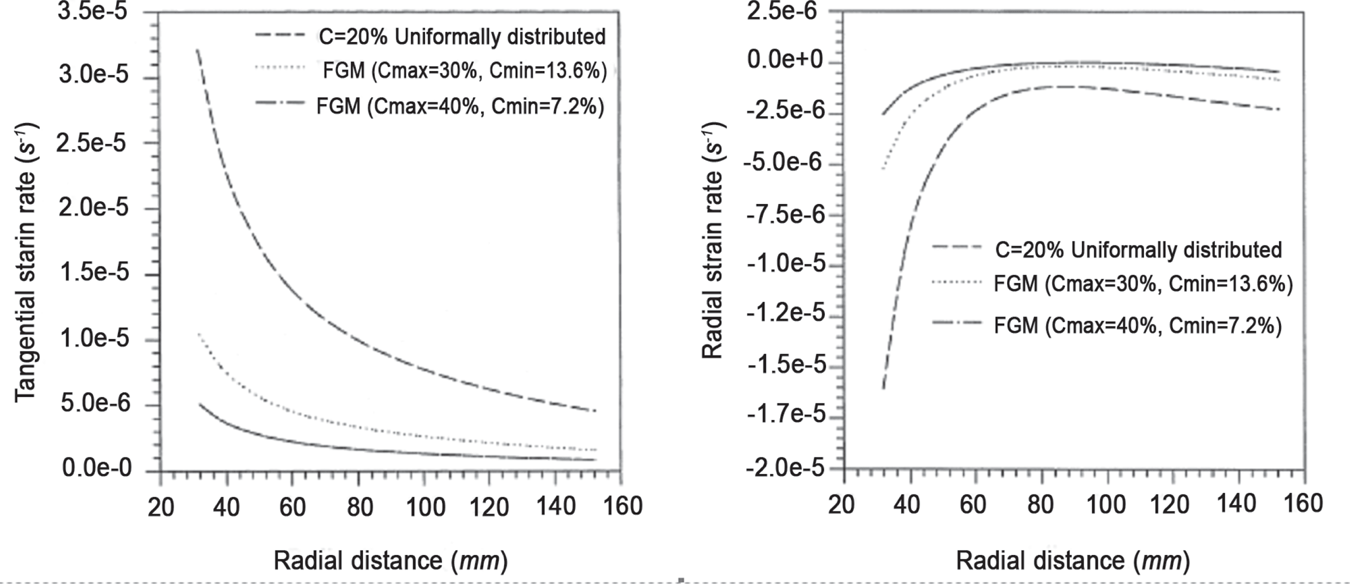
FIGURE 6.3 Variation of tangential and radial strain rate with radial distance in a particle reinforced composite disc with average particle content of 20 vol pct SiC rotating with angular velocity 15,000 rpm at 561 K for the cases when (a) particle content is uniformly distributed in the discs and (b) particle content is linearly decreasing from inner to outer radii. Content is linearly decreasing from inner to outer radii [20].

Singh and Ray [21] extended their work to the analytical treatment of anisotropy and creep in orthotropic aluminum silicon carbide composite rotating disc made of composites containing SiC whiskers under steady state using Hill yield criterion and compared with the results obtained using von Mises yield criterion for the isotropic composites. It is observed that the tangential stress distribution is lower in the middle of the disc but higher near the inner and the outer radius but the radial stress distribution does not get significantly affected due to anisotropy and also observed that anisotropy helped to reduce the tangential strain rate significantly, more near inner radius and the strain rate distribution in the orthotropic disc is lower than that in the isotropic disc following von Mises criterion. It should be noted that the anisotropy constants taken from the experimental results of other studies and the lowering of tangential creep rate may be significant in the context of real life engineering. The compressive radial strain rate also reduced in the disc following Hill criterion of yield plasticity as compared to that in isotropic disc. Thus, anisotropy appeared to help in restraining creep response both in the tangential and in the radial directions (Figure 6.4).

Eraslan and Akis [22] obtained the plane strain analytical solutions, based on Tresca’s yield criterion, for FG elastic and elastic-plastic pressurized tube problems using small deformation theory. The Young’s modulus and the uniaxial yield limit of the tube material were assumed to vary radially according to two-parametric parabolic forms. The study also investigated various types of stress states i.e., elastic, partially plastic and fully plastic. It is observed that the elasto-plastic response of the FG pressurized tube has been significantly affected by the material nonhomogenity. The non-homogeneous elasto-plastic solution has also been observed to reduce to that obtained for homogeneous one, when the material parameters were appropriately selected.

You et al. [23] analyzed steady state creep in thick-walled cylinders made of arbitrary FGM and subjected to internal pressure. The stresses and strain rates were calculated by using Norton’s creep law. The impact of radial variations of material parameters was investigated on stresses in the cylinder.

Abrinia et al. [24] obtained analytical solution to obtain radial and circumferential stresses in a functionally graded thick cylindrical vessel under the influence of internal pressure and temperature. The effect of non-homogeneity in functionally graded cylinder was analyzed in the context of achieving the lowest stress levels in the cylinder (Figure 6.5).

Thakur [25–27] have studied elastic plastic and creep transition comprehensively in structures such as rotating annular and solid discs, circular cylinders with and without inclusion, cylindrical, and spherical shells subject to various parameters such as angular speed, variable density, thermal gradients and edge loading using Seth’s transition theory. Variations in radial and circumferential stresses have been determined for different situations for compressible and incompressible materials and results for situations of fractures in subsequent situations have been inferred.

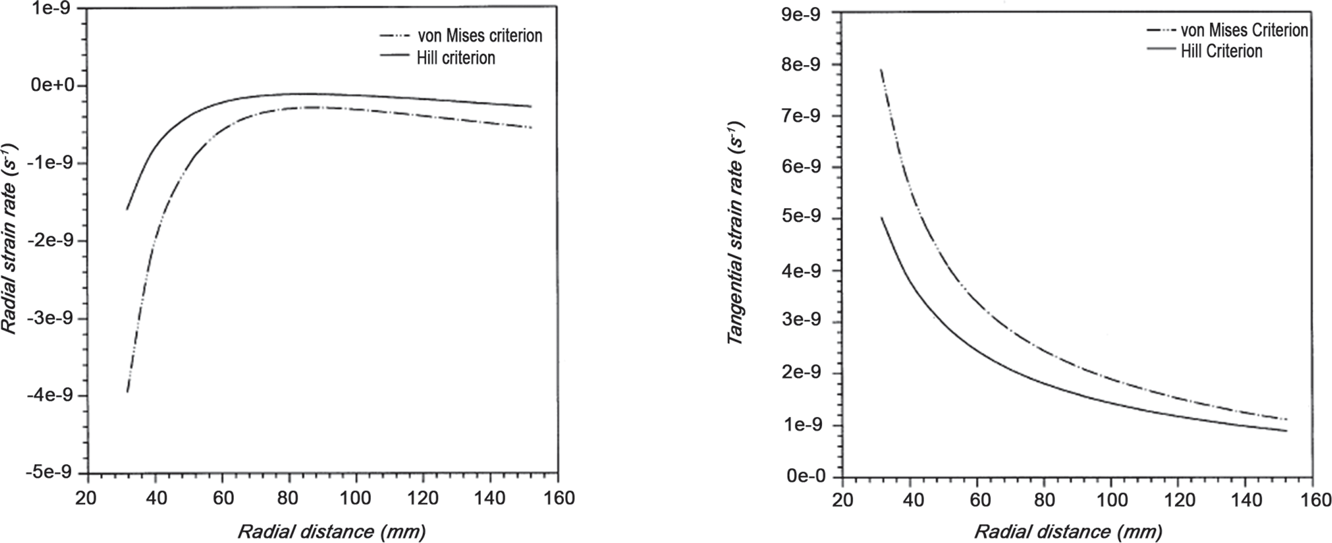
FIGURE 6.4 Variation of radial and tangential strain rates with radial distance in a rotating disc yielding according to von Mises isotropic yield criterion and Hill orthotropic yield criterion [21].

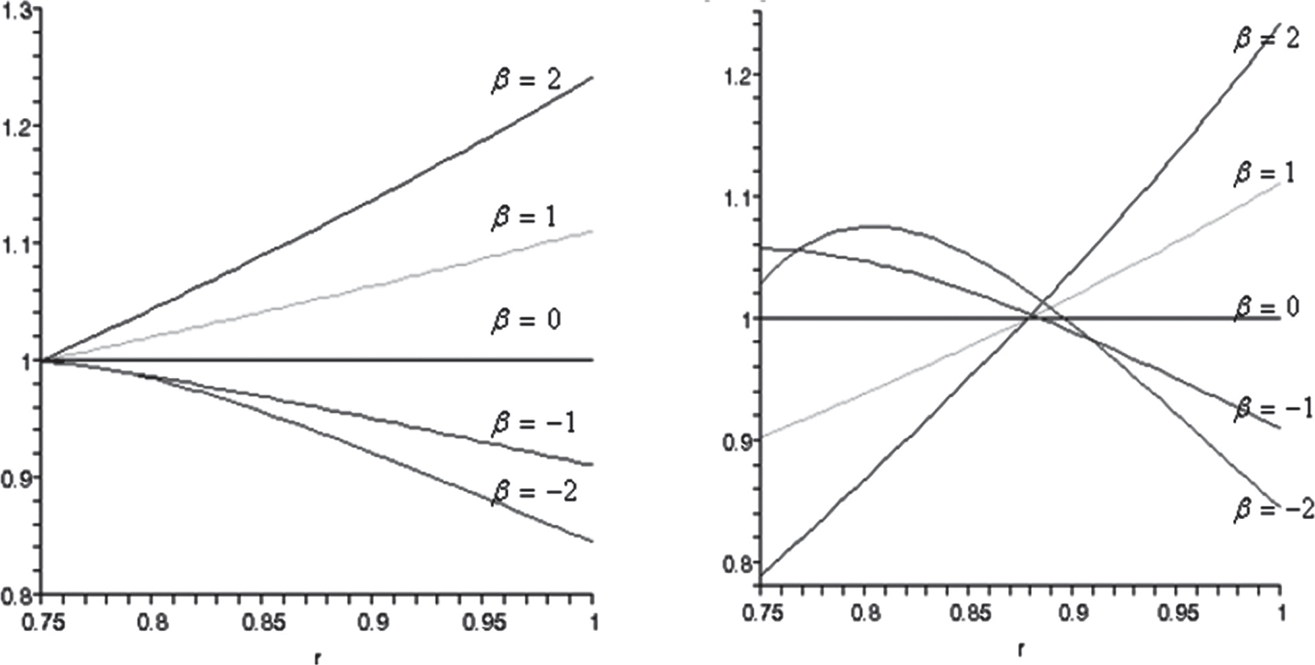
FIGURE 6.5 Variation in radial and circumferential stresses in a cylindrical vessel under the combined loading of pressure and temperature [24].

Rattan, Chamoli, Singh, and Nishi [28] studied creep behavior of anisotropic functionally graded rotating discs. They investigated the creep behavior of an anisotropic rotating disc of functionally gradient material using Hill’s yield criteria by Sherby’s constitutive model. It is concluded that the anisotropy of the material has a significant effect on the creep behavior of the FGM disc. It is also observed that the FGM disc shows better creep behavior than the non FGM disc.

Vandana and Singh [29] analyzed the effect of residual stress and reinforcement geometry in an anisotropic composite rotating disc having varying thickness. The creep analysis carried out in a rotating disc made of Al-SiC (particle/whisker) composite having hyperbolically varying thickness using anisotropic Hoffman yield criterion and results obtained are compared with those using Hill’s criterion ignoring difference in yield stresses by Sherby’s creep law for the steady state creep behavior. It is observed that the stresses are not much affected by the presence of thermal residual stress, while thermal residual stress introduces significant change in the strain rates in an anisotropic rotating disc. Secondly, it is noticed that the steady state creep rates in whisker reinforced disc with/without residual stress are observed to be significantly lower than those observed in particle reinforced disc with/without residual stress. It is concluded that the presence of residual stress in an anisotropic disc with varying thickness needs attention for designing a disc.

Nejad et al. [41] studied a closed-form analytical solution for the steady-state creep stresses of rotating thick cylindrical pressure vessels made of FGMs. Creep response of the material has been described by Norton’s Law. Exact solutions for stresses and strain rate were obtained under the plane strain condition. The effect on radial and circumferential stresses together with the equivalent strain rate in rotating thick-walled cylindrical vessels under internal pressure has been investigated. The result obtained shows that the property of FGMs has a significant influence on the equivalent creep strain rate and stresses distributions along the radial direction (Figure 6.6).

Vandana and Singh [30] studied mathematical modeling of creep in a functionally graded rotating disc with varying thickness. This study gave an analytical framework for the analysis of creep stresses and creep rates in the isotropic rotating non-FGM/FGM disc with uniform and varying thickness by Sherby’s law. The creep response of rotating disc is expressed by threshold stress with value of stress exponent as 8. The results compared for isotropic non FGM/FGM constant thickness disc with those estimated for isotropic varying thickness disc with the same average particle content distributed uniformly and suggested the distribution of stresses and strain rates becomes relatively more uniform in the isotropic FGM hyperbolic thickness disc (Figure 6.7).

Loghman et al. [31] investigated the creep behavior of composite cylinder made of polypropylene reinforced by functionally graded multi walled carbon nanotubes (FG-MWCNTs). It had been found that the radial and circumferential strains of the cylinder reduce with increasing content of carbon nanotubes. It was also concluded that the uniform distribution of MWCNTs reinforcement does not considerably influence on stresses.

Sharma and Panchal [32] considered a pressurized thick-walled functionally graded rotating spherical shell. Creep stresses were calculated under thermal effects. Transition theory and the concept of generalized measure were used to investigate these creep stresses. It was observed that angular velocity and non-homogeneity plays significant role on thermal creep stresses. Further, it was concluded that spherical shell made of thick walls is a safer prospect for designs.

Thakur et al. [33] presented exact solution of rotating disc with shaft problem in the elastoplasic state of stress having variable density and thickness by using Seth’s transition theory. It is observed that the rotating disc made of the compressible material with an inclusion requires higher angular speed to yield at the internal surface as compared to the disc made of incompressible material, and a much higher angular speed is required to yield with the increase in radii ratio. The thickness and density parameters decrease the value of angular speed at the internal surface of the rotating disc of compressible as well as incompressible materials.

FIGURE 6.6 Cross section of thick cylindrical vessel with variable thickness [35].

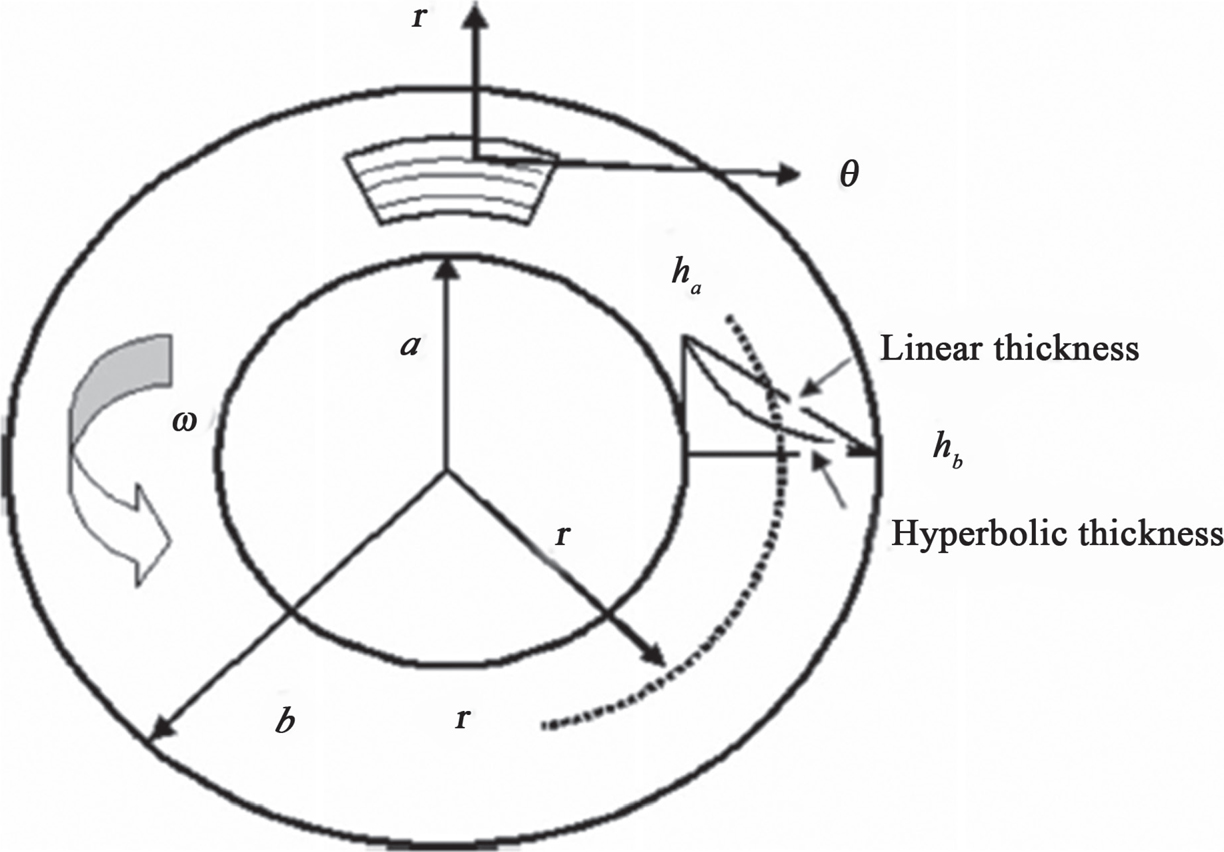
FIGURE 6.7 Geometry of the disc showing variation in thickness [30].

6.3 DISCUSSIONS AND CONCLUSION

The linear theory has given rise to a vast amount of important results which have been corroborated by experiments more exactly than one may expect, covering all types of structural components. Elastic-plastic transition is obtained in current literature with the help of a semi-empirical yield condition like that of Tresca or Von-Mises. The stresses are obtained from the elastic solution and then substituted in the yield condition to get the transition surface. The possibility of treating it as a transition or turning point phenomenon in finite deformation has not been explored. When the plastic state tends to set in, the stress-strain relation undergoes a change. This is reflected in the equations. The linear classical theory cannot do it. In the transition state whole of the material participates, and not simply a selected region or a line as assumed by classical theories. The demands of high speed technology in transportation, communication, and energy conversion have forced us to take serious notice of non-linearity. Since this non-linearity is difficult to investigate, workers have taken to the artifice of replacing it by singular, non-differentiable, or discontinuous surfaces. This piecewise treatment necessitates the use of adhoc and semi-empirical law, which may or may not exist. Linearizing non-linear problems by perturbation, boundary layer and other techniques do not provide satisfactory explanation for some important characteristics of non-linearity. As a result, a number of important physical effects do not get adequate scientific expression. There is hardly any information which we do not know about linear fields. Their existence, uniqueness, and stability are well established. Nature does not always confirm to our abstract concepts of linearity, smoothness, symmetry, identity, and isotropy. It is true that physical phenomena tend to behave linearly in course of time, which may be millions of years. Thus transitions, which frequently occur in nature, have to be tackled. In fact, all inter-disciplinary fields which are so important in modern research give rise to important transition problems. Hence, both the macro and micro analysts must devote attention to non-linearity involved in the subject.