9.1 INTRODUCTION

A rotating disc is a common component in turbines, gas turbine rotors, compressors, turbo generators, flywheel, aero-engines, rotors, automobiles, computer’s disc drive, and other dynamic applications are usually operated at relatively higher angular speed and subjected to high temperature. Materials of discs are required to sustain steady loads for a long period of time under different temperature conditions. In such conditions, the material may continue to creep until its usefulness is seriously impaired. As a result, a number of researchers have studied the creep behavior in composite materials with the property of superior heat resistance. The effect of anisotropy on the stress and strain rates have been studied and concluded that the anisotropy of the material has a significant effect on the creep of a rotating disc [1]. The steady-state creep response of an isotropic FGM disc with constant thickness by using Sherby’s constitutive model have been analyzed and the results obtained for nonlinear variation of particle distribution along the radial distance of the disc are compared with that of discs containing the same amount of particle distributed uniformly or linearly along with the radial distance [17]. Hasan Callioglu et al. [18] studied that stress analysis on functionally graded rotating annular discs subjected to temperature distributions parabolically decreasing with radius. He concluded that with the increase in temperature, the tangential stress component gets decreased at the inner surface but increased at the outer surface whereas the radial stress component gets reduced gradually for all the temperature distributions. The problem of rotating disc with variable thickness, thermal effect, heat generation effect, and pressure by using Seth’s transition theory has been studied [2, 19–21]. Gupta et al. [3] discuss the variation of Poisson ratios and thermal creep stresses and strain rates in an isotropic disc. Kaur et al. [4] study steady thermal stresses in a thin rotating disc of infinitesimal deformation with edge loading. An attempt has been made to investigate steady-state creep behavior of thermally graded isotropic discs rotating at elevated temperatures. The results are compared with the disc having a uniform temperature profile from inner to the outer radius and are displayed graphically in a designer-friendly format for the said temperature profiles. It is observed that there is a need to extend the domain of thermal gradation for designing rotating discs [22]. A theoretical solution for time-dependent thermo-elastic creep analysis of a functionally graded thick-walled cylinder based on the first-order shear deformation theory is presented. The effects of the temperature gradient and FG grading index on the creep stresses of the cylinder are investigated. A numerical solution using the finite element method is also presented and good agreement was found [5]. Keeping this in mind, the study ends with an effort to determine the plastic stress and strain analyses for the particle reinforced isotropic/anisotropic disc with constant thickness in presence of thermal gradients and compare it with those isotropic/anisotropic discs with the operating under isothermal conditions. The analysis has been done by using von Mises criteria/Hill’s criterion for yielding. The creep response of the disc under stresses developing due to rotation has been determined using Sherby’s law. The material parameters of creep vary along the radial direction in the disc due to varying composition.

Keeping this in mind, the study ends with an effort to determine the creep behavior for the particle reinforced anisotropic disc with constant thickness in presence of thermal gradients and compare it with those anisotropic discs with the operating under isothermal conditions.

In this chapter, the steady-state creep has been analyzed in composite disc made of material 6061Al base alloy containing 20 vol% of SiC particle. The creep behavior has been described by Sherby’s constitutive model. The analysis has been done for particle reinforced isotropic disc with hyperbolic thickness.

9.2 DISC GEOMETRY AND REINFORCEMENT PROFILE

The present study assumes composite disc having a hyperbolically varying thickness is assumed to be of the formml:

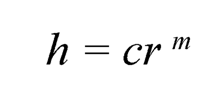(9.1)

where: c and m = –0.74 are constants.

Since the volume of disc having hyperbolically varying thickness is assumed equal to the volume of constant thickness disc, therefore;

(9.2)

The thickness of the disc is assumed to be h and a and b be inner and outer radii of the disc respectively. Let I and I₀ be the moment of inertia of the disc at inner radius a and outer radius r and b, respectively. A and A₀ be the area of cross-section of the disc at inner radius a and outer radius r and b, respectively. Here,

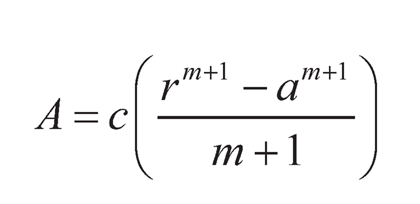(9.3)

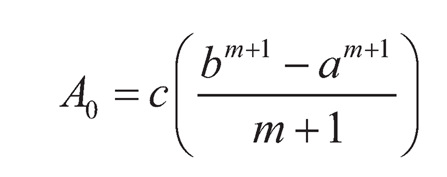(9.4)

(9.5)

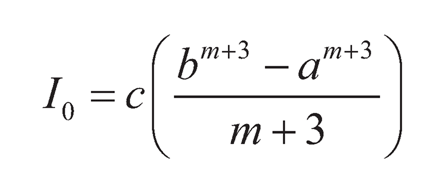(9.6)

The temperature gradient originating due to the braking action of the discs has been obtained by Finite Element Analysis. The temperature T(r), obtained at any radius r is presented below in the form of regression equation as:

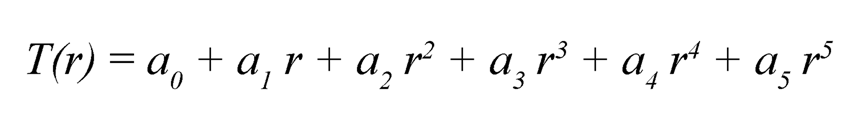(9.7)

where the coefficients a₀, a₁, a₂, a₃, a₄ and a₅ for different disc are given below:

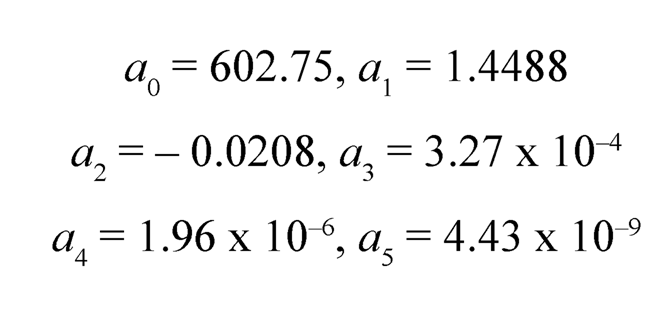9.3 ASSUMPTIONS IN VARIABLE THICKNESS DISC

Consider an aluminum silicon-carbide particulate composite disc of constant thickness h having an inner radius, a and outer radius, b rotating with angular velocity, ω(radian/sec). From symmetry considerations, principal stresses are in the radial, tangential, and axial directions. For the purpose of analysis, the following assumptions are made:

1. Stresses at a radius of the disc remain constant with time, i.e., steady-state condition of stress is assumed.

2. Elastic deformations are small for the disc and can be neglected as compared to the creep deformations.

3. Biaxial state of stress (σ_z= 0) exists at any point in the disc.

4. Frictional shear stress-induced due to braking action is estimated to be 10⁵ MPa, which is very small compared to creep stresses and therefore, can be neglected.

5. The composite shows a steady-state creep behavior which may be described by following Sherby’s law [6],

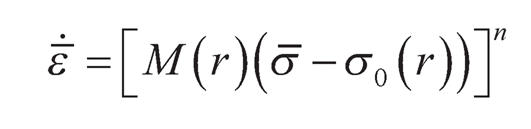(9.8)

where, is the creep parameter and ε̄̇, σ̄, n, σ₀ (r), A, D_λ, λ, b_r, E are the effective strain rate, effective stress, the stress exponent, threshold stress, a constant, lattice diffusivity, the subgrain size, the magnitude of burgers vector, Young’s modulus.

The values of material parameters M(r) and σ₀ (r) in terms of P,T(r) and V have been obtained from the creep results by using the experimental results reported by Pandey et al. [7] for Al-SiCp composite under uniaxial loading using the following regression equations:

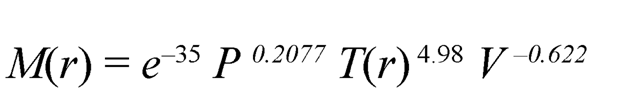(9.9)

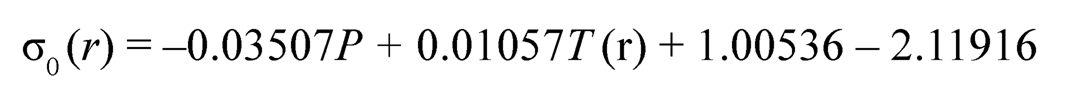(9.10)

In a FGM disc, with the creep parameters M(r) and σ₀(r) will vary radially due to variations in temperature T(r). In the present study, the particle size (P) and the particle content (V) are taken as 1.7 μm and 20% over the entire disc. Thus, for a given FGM disc under known temperature both the creep parameters are functions of radial distance and their values M(r) and σ₀(r) at any radius (r), could be determined by substituting the values of particle size, particle content, and temperature distributions into Eqs. (9.9) and (9.10), respectively.

9.4 MATHEMATICAL FORMULATION

The generalized constitutive equations for creep in an anisotropic composite disc under multiaxial stress takes the following formml:

(9.11)

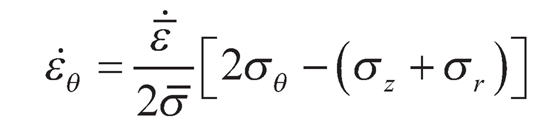(9.12)

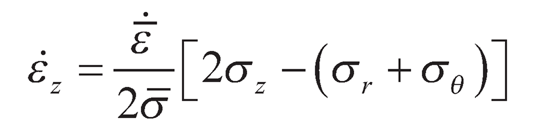(9.13)

where ε̇_r, ε̇_θ, ε̇_zand σ_r, σ_θ, σ_z are the strain rates and the stresses respectively in the direction r, θ and z. ε̄̇ be the effective strain rate and σ̄ be the effective stress. For biaxial state of stress (σ_r,σ_θ ) the effective stress is:

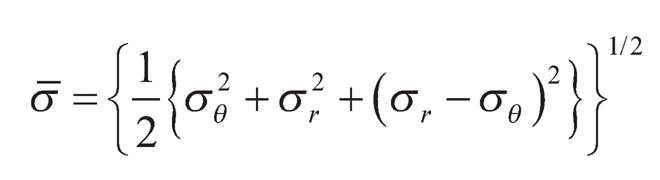(9.14)

Using Eqs. (9.8) and (9.14), Eq. (9.11) can be rewritten as:

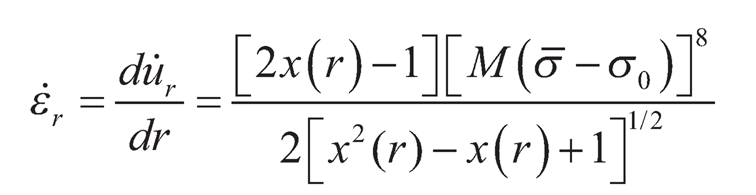(9.15)

Similarly from Eq. (9.12):

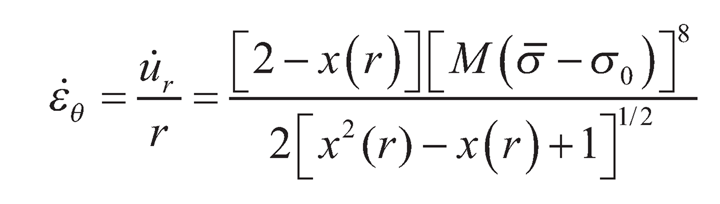(9.16)

(9.17)

where, 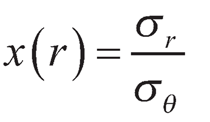is the ratio of radial and tangential stresses at any radius r.

Dividing Eq. (9.15) by Eq. (9.16), we get:

(9.18)

The equation of equilibrium for a rotating disc with varying thickness can be written as:

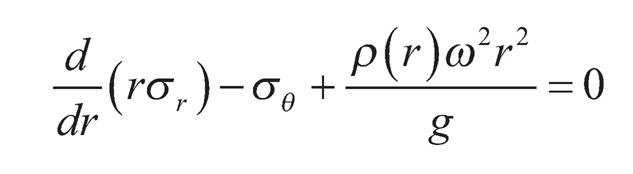(9.19)

where ρ(r) is the density of FGM disc.

Boundary conditions are:

(9.20)

We get the tangential stress σ_θ from Eq. (9.19) by using Eq. (9.15) and Eq. (9.16):

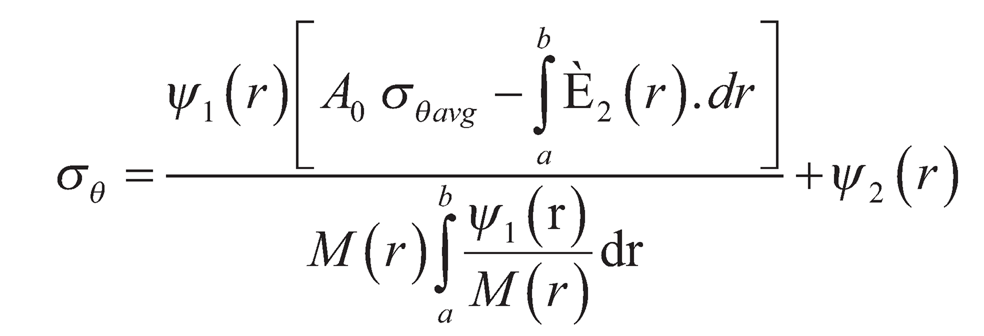(9.21)

where,

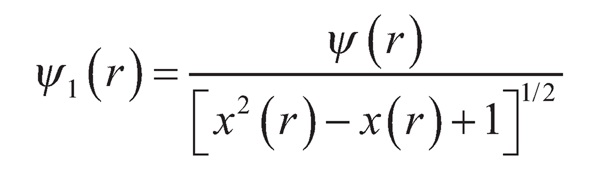(9.22)

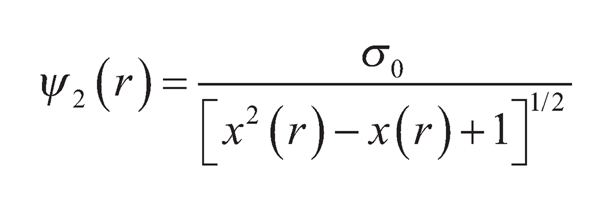(9.23)

and

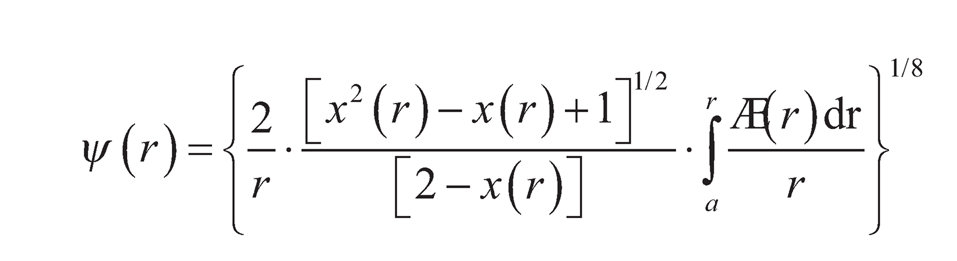(9.24)

The average tangential stress may be defined as:

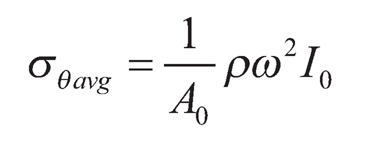(9.25)

Now σ_r(r) can be obtained by integrating Eq. (9.18) within limits a to b:

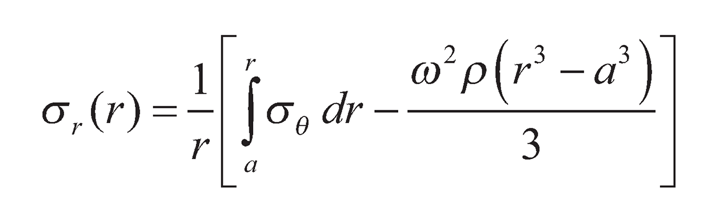(9.26)

Thus, the tangential stress σ_θ and radial stress σ_r are determined by Eqs. (9.21) and (9.26) respectively, for anisotropic disc with constant thickness. Then strain rates ε̇_r, ε̇_θ and ε̇_z calculated from equations (9.15), (9.16) and (9.17).

9.5 NUMERICAL COMPUTATION

The stress distribution is evaluated from the above analysis by the iterative numerical scheme of computation. For rapid convergence, 75% of the value of σ_θ (r) obtained in the current iteration has been mixed with 25% of the value of σ_θ (r) obtained in the last iteration for the use in the next iteration.

9.6 RESULTS AND DISCUSSION

The stress exponent and density of disc material have been taken as n = 8 and ρ = 2812.4kg/m³, respectively. A computer program based on the mathematical formulation has been developed to obtain the steady-state creep response of the rotating isotropic discs operating under the thermal gradient. The tangential stress operating under a thermal gradient is a little higher near the inner radius and slightly lowers near the outer radius as compared to the disc without thermal gradients as shown in Figure 9.1.

The radial stress developing due to rotation in the isotropic disc operating under a thermal gradient is higher over the entire radius as compared to the isotropic disc without thermal gradients as shown in Figure 9.2. Although, the variation in the magnitude of tangential as well as radial stress distribution is very small in the isotropic discs due to the presence of thermal gradients. In Figure 9.3, the tangential strain rate decreases significantly over the entire radius in the isotropic discs operating under the thermal gradients compared to the discs without thermal gradients. Although, the tangential stress in disc under the thermal gradients is higher near the inner radius than the disc under thermal gradients as shown in Figure 9.4, but lower operating temperature near the inner radius of the disc with thermal gradients is able to reduce the creep rate overcoming the effect of higher stress. In Figure 9.4, the effect of imposing thermal gradients on the radial strain rate in the isotropic discs is similar to that observed for the tangential strain rate. The magnitude of the radial strain rate firstly increases rapidly with radial distance and then starts decreasing.

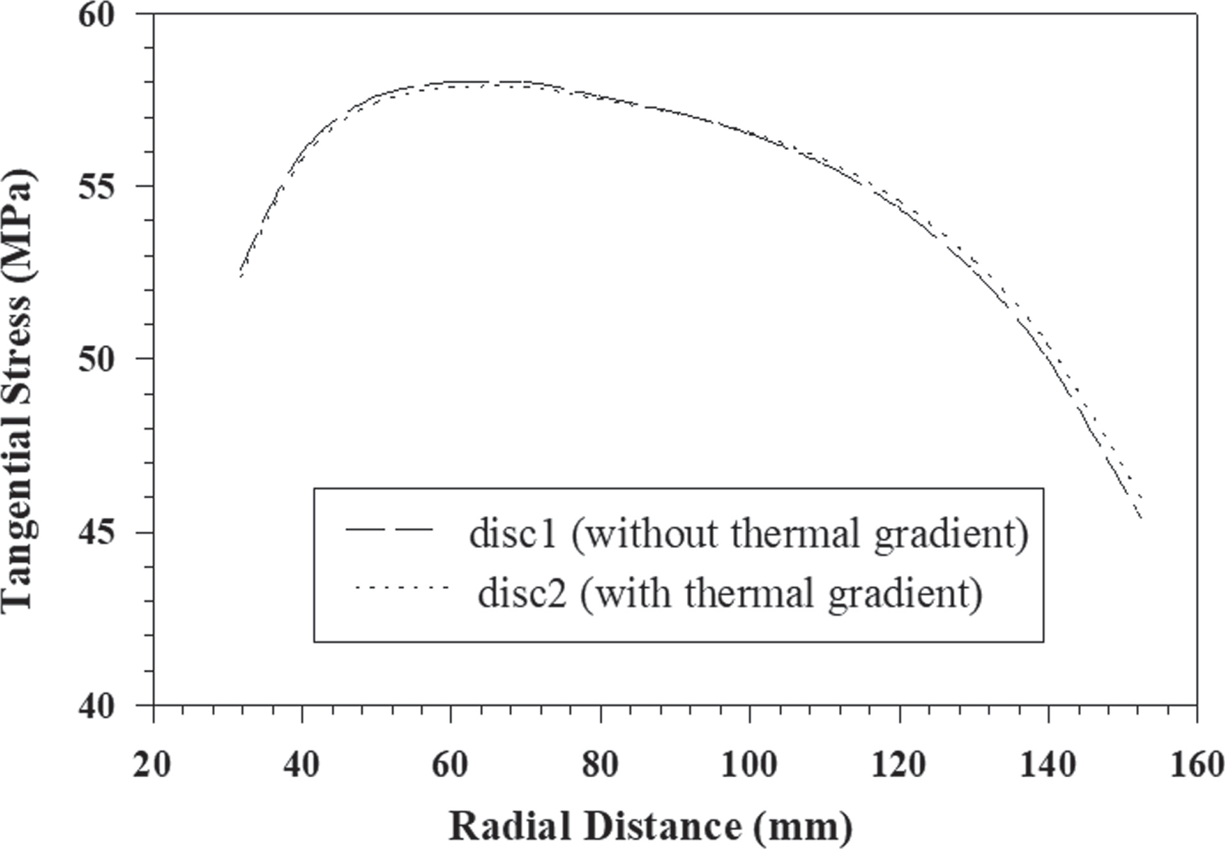
FIGURE 9.1 Variation of tangential stress along with radial distance in composite hyperbolically varying discs with/without thermal gradient.

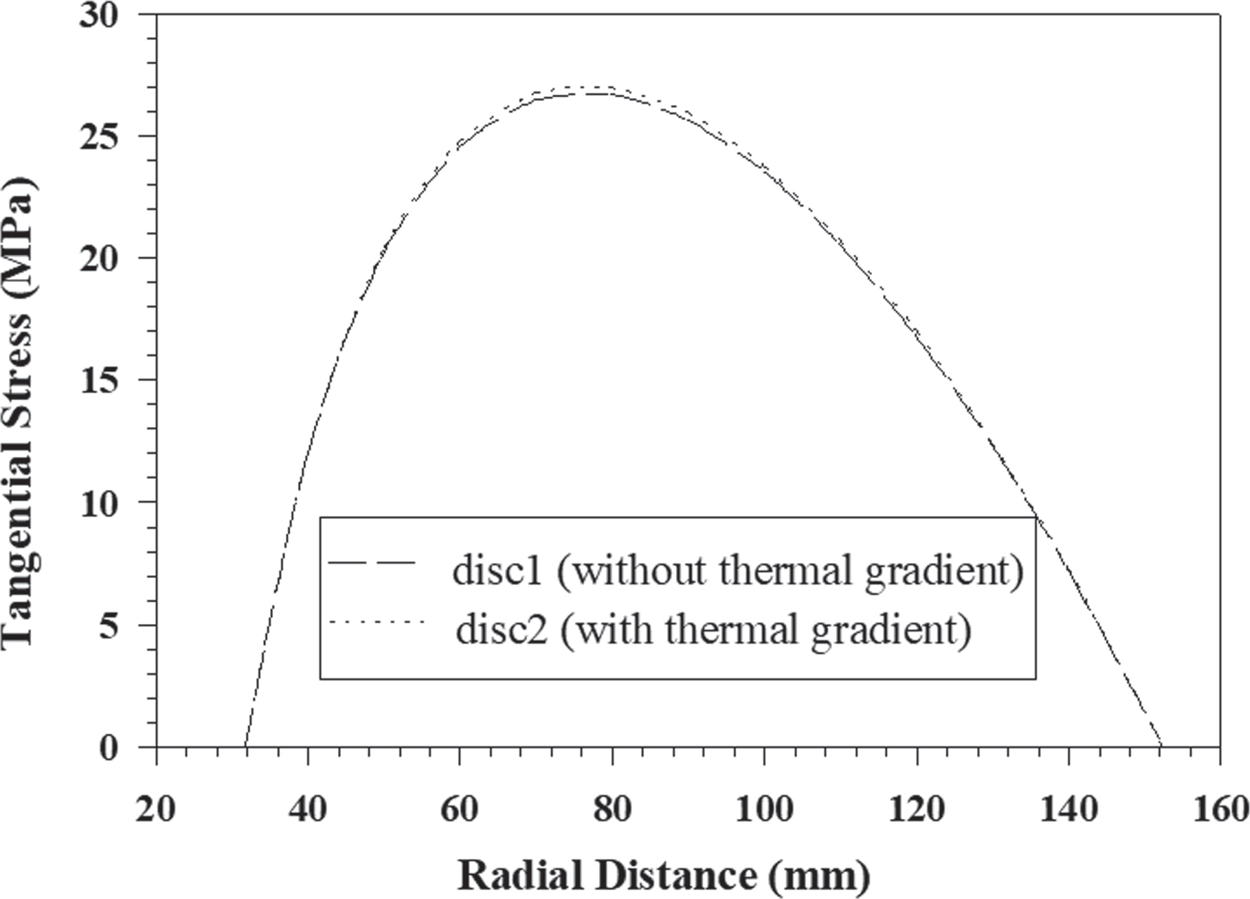
FIGURE 9.2 Variation of radial stress along with radial distance in composite hyperbolically varying discs with/without thermal gradient.

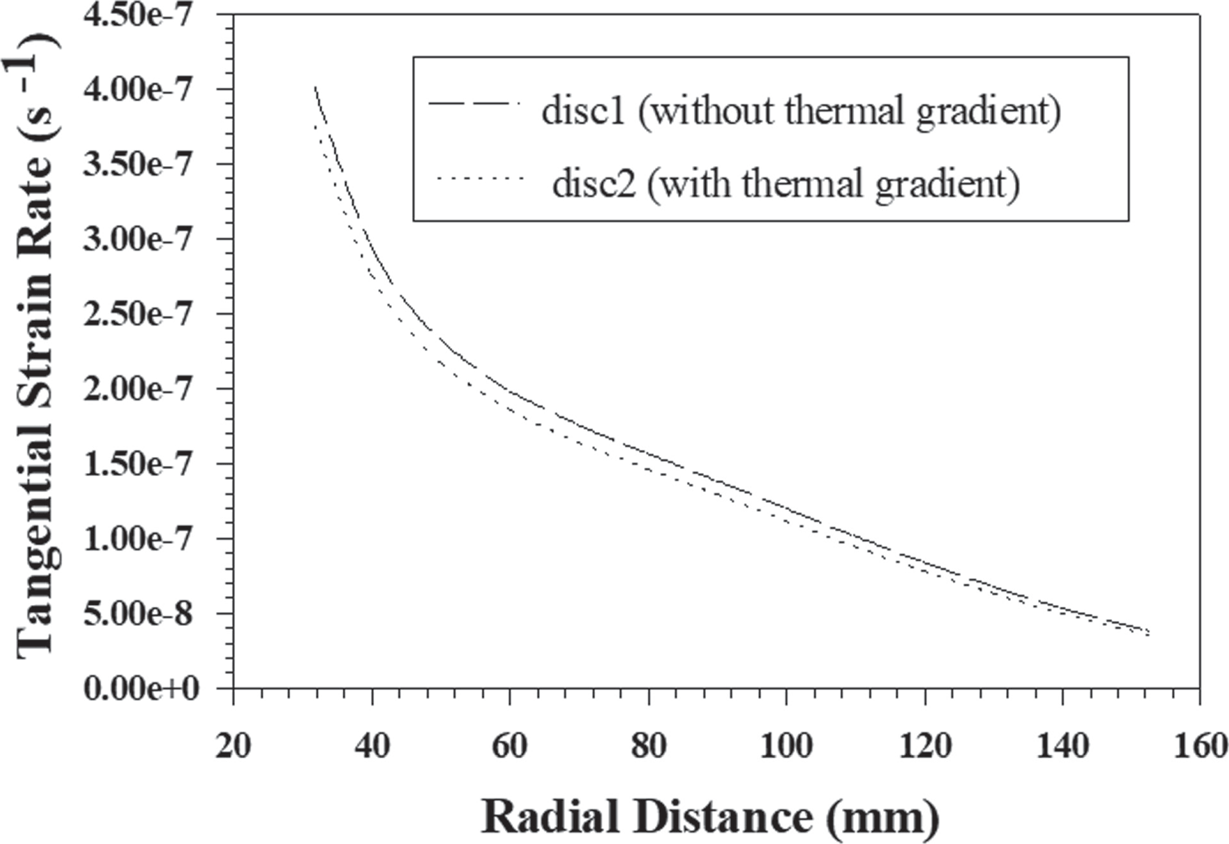
FIGURE 9.3 Variation of tangential strain rate along with radial distance in composite hyperbolically varying discs with/without thermal gradient.

FIGURE 9.4 Variation of radial strain rate along with radial distance in composite discs with/without thermal gradient.

9.7 CONCLUSION

From the above discussion, it can be concluded that:

1. The thermal gradients significantly affect the strain rate distribution in an isotropic particle reinforced disc having a hyperbolic thickness, but its effect on the distribution of stresses is relatively small.

2. The thermal gradient plays a significant role in developing the creep strains, it may be taken care of while design a rotating disc.

KEYWORDS