7.1 INTRODUCTION

Zirconia (ZrO₂) has been considered as a wear-resistant and osteoconductive ceramic, highly suitable for making stress-bearing crowns of dental implants. Various properties, namely, less inflammatory response, compatibility of zirconia in contact with gum tissues, lower plaque retention, and highly aesthetic tooth-like coloration has made zirconia a suitable alternative to titanium implants [2, 6, 19]. The production of ceramic dental implants have improved in past few years [7, 20]. The yttria-stabilized tetragonal zirconia polycrystal, popularly known as Y-TZP has been a preference for some years now, having the highest fracture strength [10, 12, 15, 27]. Muhammad et al. [11] confirmed in their chapter that zirconia is highly flexible in all directions of the lattice plane. The Poisson ratio obtained, i.e., from 0.16 to 0.31 also indicate high anisotropy. The stiffness constants so obtained will also be used in this chapter for the determination of elastic-plastic transitional stresses.

This chapter is concerned with the investigation of elastic-plastic transition stress in Zirconia-based crowns of ceramic dental implants, further comparing the results with stresses in titanium-based implants. The chapter also checks the similarities between the implants and human tooth enamel using Seth’s transition theory. The crowns will be modeled as spherical shells exhibiting transversely isotropic macrostructural symmetry. Equations for modeling spherical shells made of isotropic materials are available in most standard textbooks [3, 9, 13, 14, 17, 29]. Following the classical methods of stress and strain determination, Miller [16] evaluated solutions for stresses and displacements in a thick spherical shell subjected to internal and external pressure loads. You et al. [30] presented a highly precise model to carry out elastic analysis of thick-walled spherical pressure vessels. The authors have studied the behavior of shells particularly when some assumptions, such as (i) incompressibility of material used, (ii) creep strain law derived by Norton, (iii) yield condition of Tresca, and (iv) associated flow rules; were made. The need of utilization of these specially appointed semi-experimental laws in elastic-plastic transition depends on approach that the transition is a linear phenomenon which is unrealistic. Deformation fields related with the irreversible phenomenon, such as elastic-plastic disfigurements, creep relaxation, fatigue, and crack, etc. are non-linear in character. The traditional measures of deformation are not adequate to manage transitions. The concept of generalized strain measures and transition theory given by Seth [21] has been applied to find elastic-plastic stresses in various problems by solving the non-linear differential equations at the transition points. Shahi and Singh [24] successfully calculated elastic-plastic transitional stresses in human tooth enamel and dentine using this theory. The results for hydroxyapatite (HAP)_{-Ca10(PO4)6(OH)2,} which structures 95% of enamel and 50% of dentine by weight, were also obtained for comparative analysis. The theory has been used to solve various problems of stress and strain determination in structures modeled in the form of discs and shells [25, 28]. All these problems based on the recognition of the transition state as separate state necessitates showing the existence of the used constitutive equation for that state.

7.2 GOVERNING EQUATIONS

We consider a spherical shell of constant thickness with internal and external radius a and b respectively under external pressure p. The external pressure will act radially to simulate the state of axial compression (Figure 7.1).

FIGURE 7.1 Structure of the crown part of the implant.

1. Displacement Coordinates: The components of displacement in spherical coordinates (r, θ, ø) are taken as:

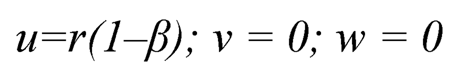(7.1)

where: ß is position function depending on r.

The generalized components of strain are given by Seth [21, 22] as:>

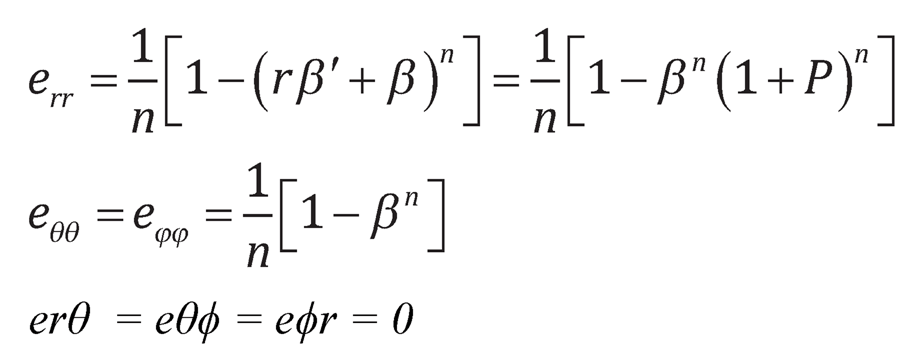(7.2)

where: n is the measure and rαβ’ = βP; P is a function of ß and ß is a function of r.

2. Stress-Strain Relation: The stress-strain relations for isotropic material are given by Sokolinokoff [26]:

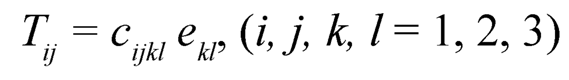where T_ij and e_kl are the stress and strain tensors respectively. These nine equations contain a total of 81 coefficients e_ijkl, but not all the coefficients are independent. The symmetry of T_ij and e_ij reduces the number of independent coefficients to 36. For Transversely isotropic materials which have a plane of elastic symmetry, these independent coefficients reduce to 5. The constitutive equations for transversely isotropic media are given by Altenbach et al. [1]:

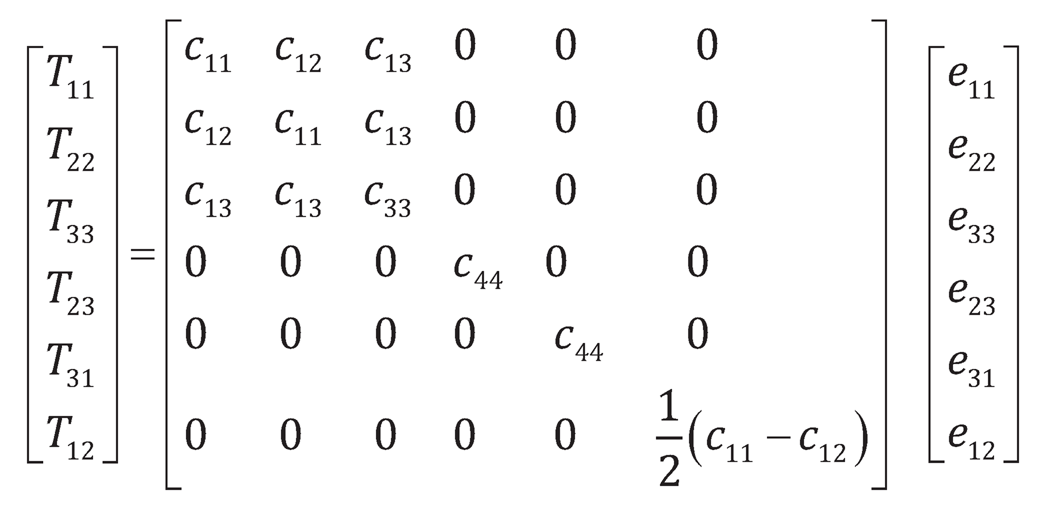(7.3)

Substituting (Eqn. 2) in (Eqn. 3), we get:

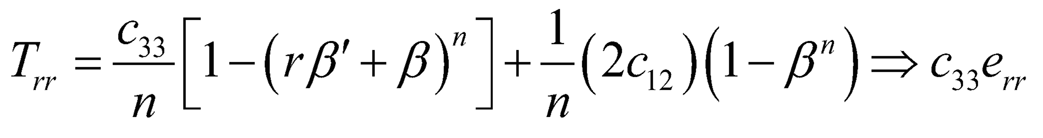(7.4)

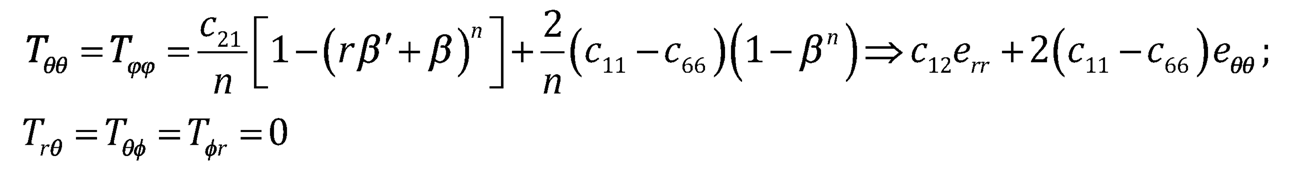3. Equation of Equilibrium: The equations of equilibrium are:

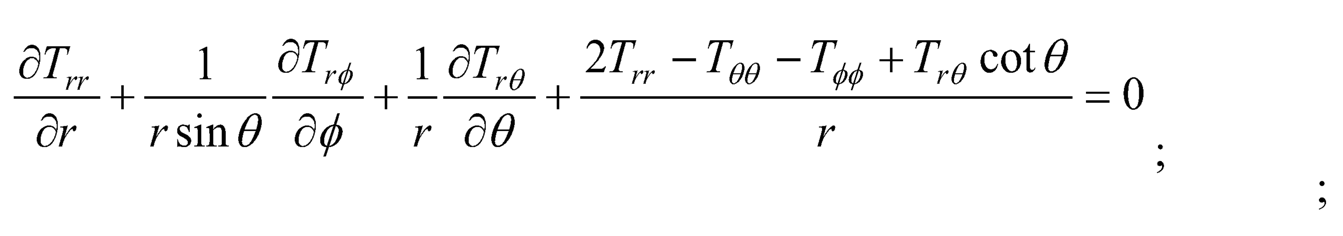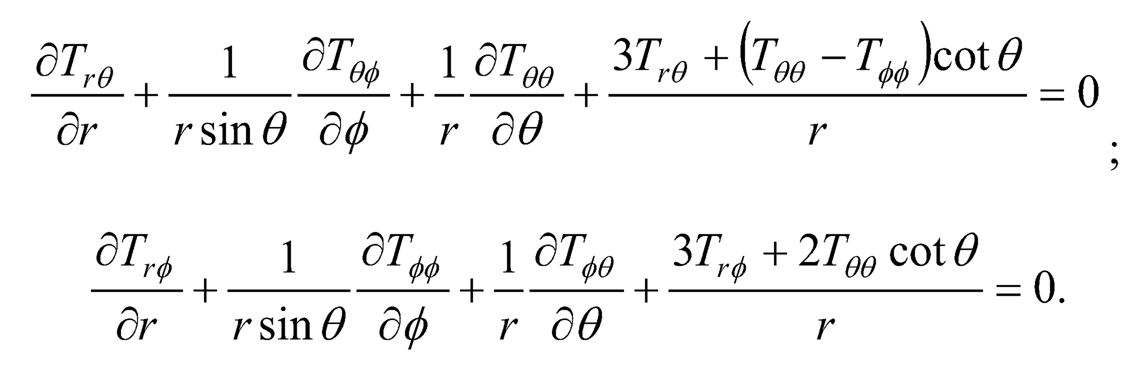(7.5)

Substituting (Eqn. 4) in (Eqn. 5), we see that the equations of equilibrium are all satisfied except:

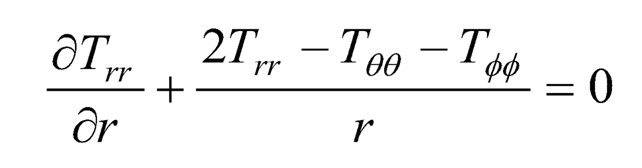(7.6)

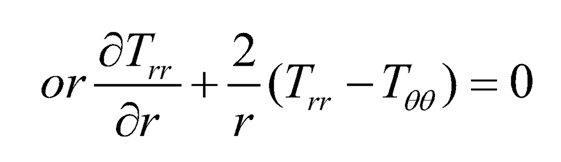(7.7)

From (Eqn. 7), one may also say that:

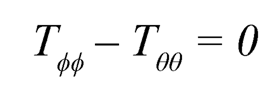(7.8)

(Eqn. 8) is satisfied by T_θθ and T_ϕϕ as given by (Eqn. 2). If c₂₁ = c₃₁, c₂₂– c₃₃– c₃₂– c₂₃ the equation of equilibrium from (Eqn. 6) becomes:

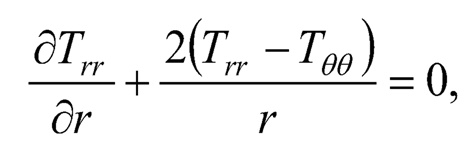(7.9)

4. Critical Points or Turning Points: By substituting (Eqn. 4) into (Eqn. 9), we get a non-linear differential equation in terms of β:

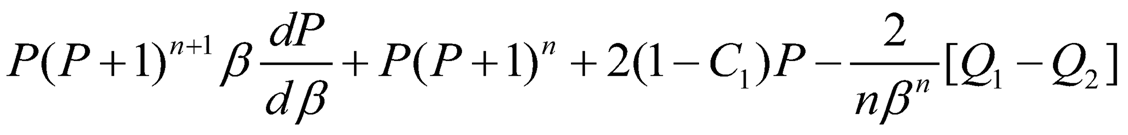(7.10)

where;

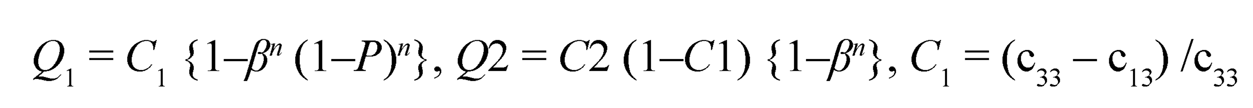and

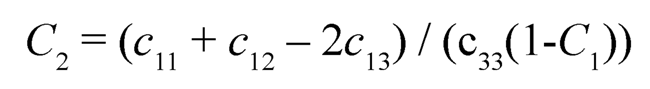where P is function of ß and ß is function of r only.

5. Transition Points: The transition points of ß in (Eqn. 10) are P = 0, P → –1 and P → ± ∞

    To solve the Elastoplastic stress problems we consider the case of P → ± ∞

6. Boundary Condition: The boundary conditions of the problem are given by:

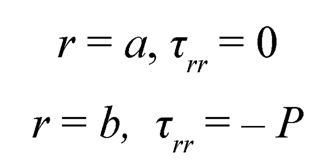(7.11)

7.3 PROBLEM SOLUTION

For finding the elastic-plastic stresses, the transition function is taken through the principal stresses at the transition point P → ± ∞, we define the transition function ζ as:

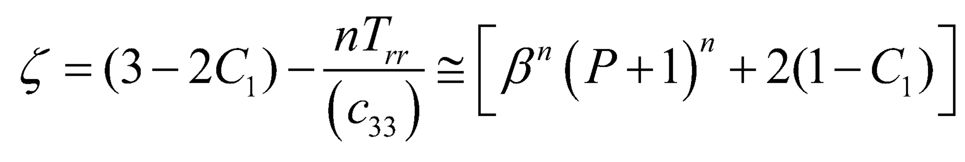(7.12)

where ζ be the transition function unction of r only. Taking the logarithmic differentiation of (Eqn. 12), with respect to r and using (Eqn. 10), we get:

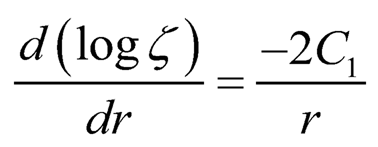(7.13)

Taking the asymptotic value of (Eqn. 13) as P → ± ∞ and integrating, we get:

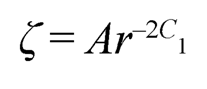(7.14)

where A is a constant of integration and C₁ = (c₃₃ – c₁₃)/c₃₃. From (Eqn. 12) and (7.14), we have:

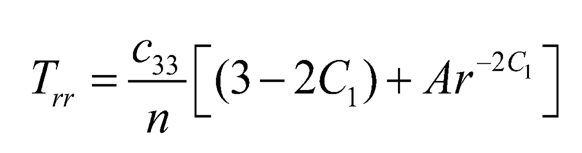(7.15)

Using boundary condition from (Eqn. 11) in (Eqn. 15), we get:

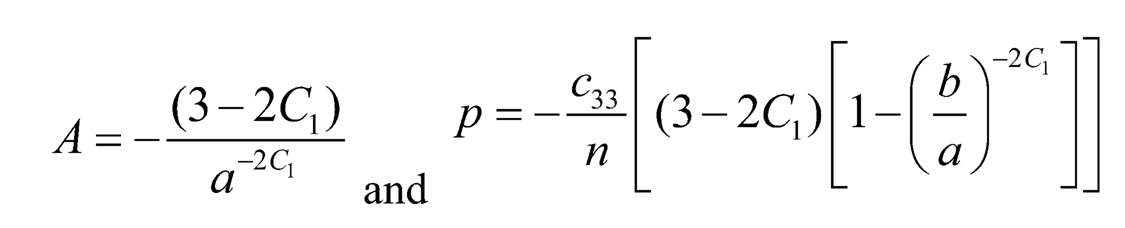(7.16)

Substituting (Eqn. 16) in to (Eqn. 15) and using (Eqn. 16) in equation of equilibrium, we get:

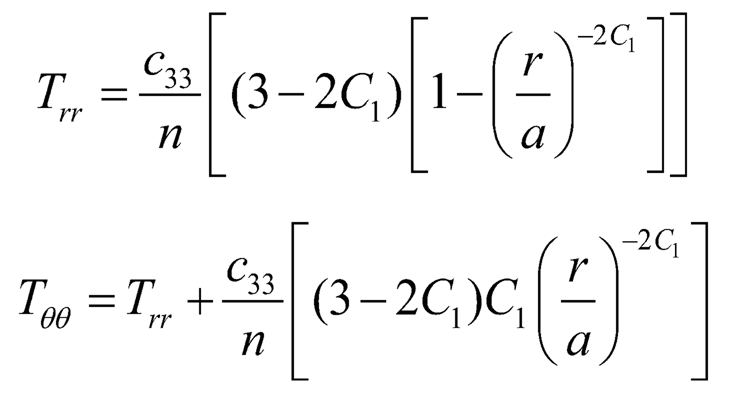(7.17)

1. Initial Yielding: From (Eqn. 17), it is seen that |T_θθ–Trr| is maximum at the outer surface (that is at r = b), therefore yielding of the shell will take place at the external surface of the shell:

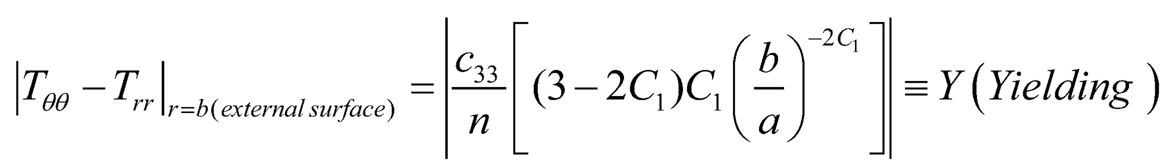(7.18)

Using (Eqn. 18) in Eqns. (7.15)–(7.17), we get the transitional stresses as in non-dimensional components as:

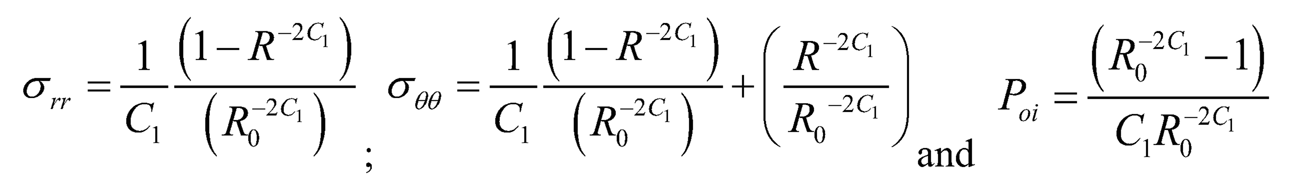(7.19)

where;

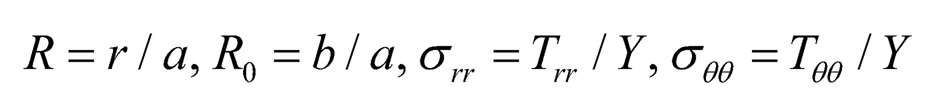and

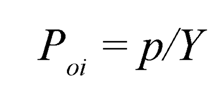2. Fully-Plastic State: For fully-plastic case [23], C₁ → 0; therefore stresses and pressure from (Eqn. 19) becomes:

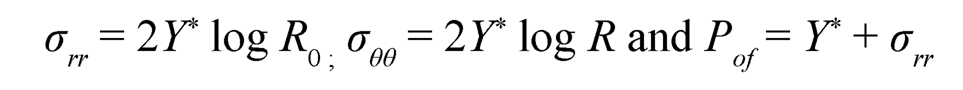(7.20)

where,

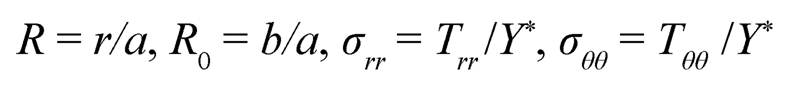and

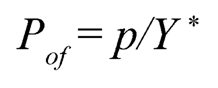7.4 NUMERICAL RESULTS AND DISCUSSION

The above investigations elaborate the initial yielding and fully plastic state of a crown made of zirconia and titanium modeled in the form of spherical shell subjected to external pressure, to analyze uniaxial compression. The elastic constants for the same are taken from the literature [11] which has been obtained by ultrasonic resonance spectroscopy, a nondestructive measure to obtain the stiffness constants. The results obtained for both types of crowns are compared with enamel. Enamel is made up of HAP mineral, 95% by vol. All these materials exhibit transversely isotropic macrostructural symmetry.

In Figure 7.2, the curves are plotted for pressure at initial yielding at various radius ratios. It is observed that the intensity of pressure at initial yielding increases with an increase in the thickness of the shell. It has been observed that titanium had the lowest yield strength and yielded at lower levels of stress as compared to enamel and Zirconia. Figures 7.3 and 7.4 show the trends of radial and circumferential stresses at initial yielding. Maximum stresses were observed at the external surface of the shell. In Figure 7.5, the curves are plotted for the pressure required at a fully plastic state for various radius ratios. It has been observed that shells exhibited high plasticity when the thickness of the shell was between ratios 1 < R₀ < 3, particularly Zirconia. A significant drop in the levels of plasticity is observed when the thickness increases. The plasticity of Zirconia is inferred to be greater than that of titanium. Figures 7.6 and 7.7 represent the trends of radial and circumferential stresses at a fully plastic state. The observations infer to the fact that the principal stress differences were maximum at the external surface of the crowns.

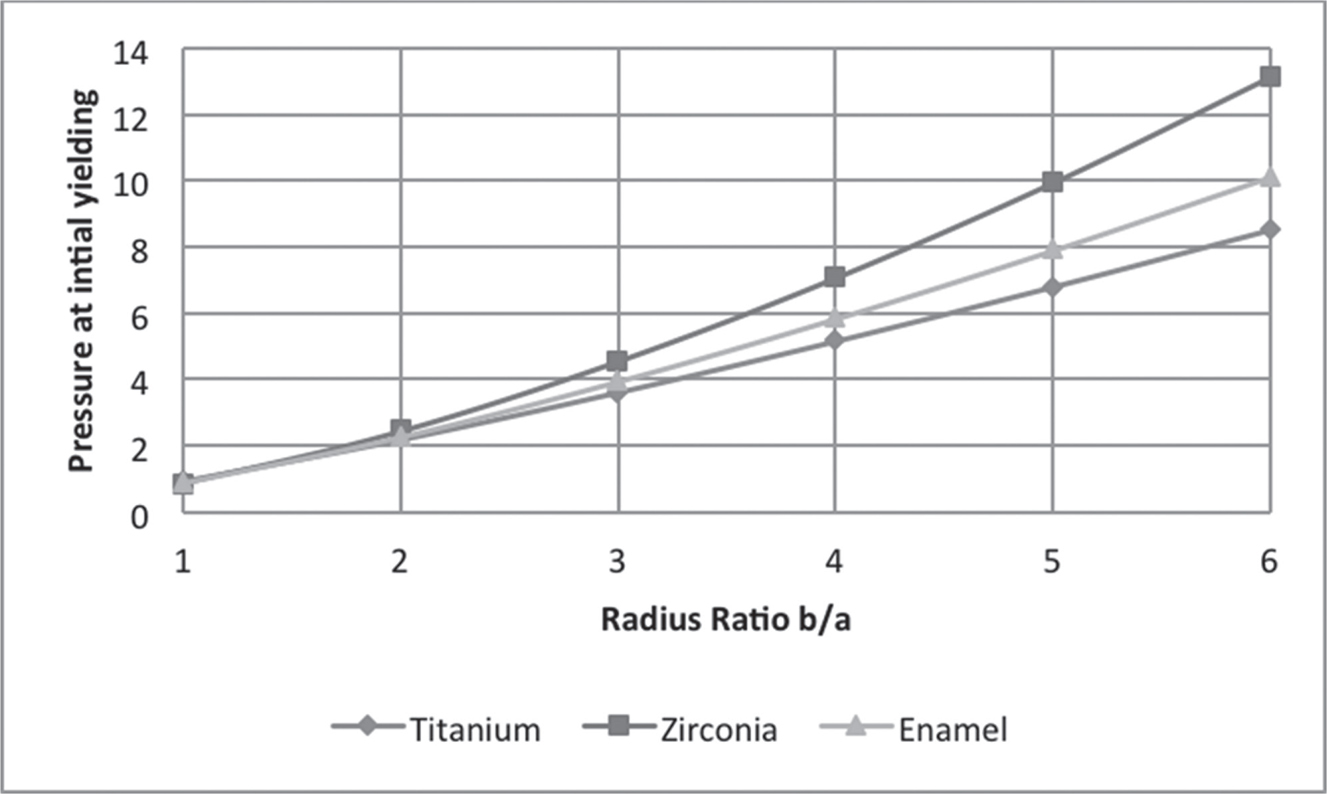
FIGURE 7.2 Pressure in the Shell at initial yielding for radius ratio R₀.

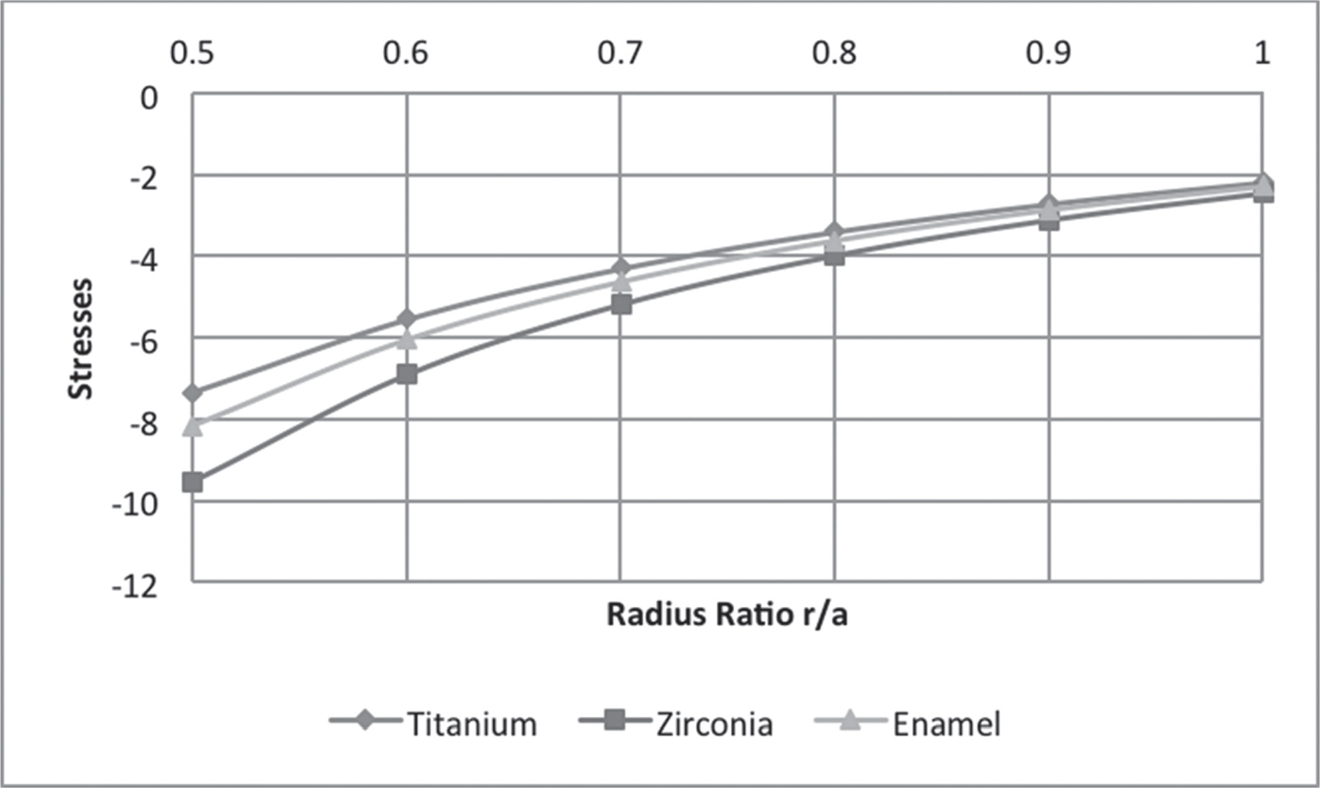
FIGURE 7.3 Radial stresses at initial yielding.

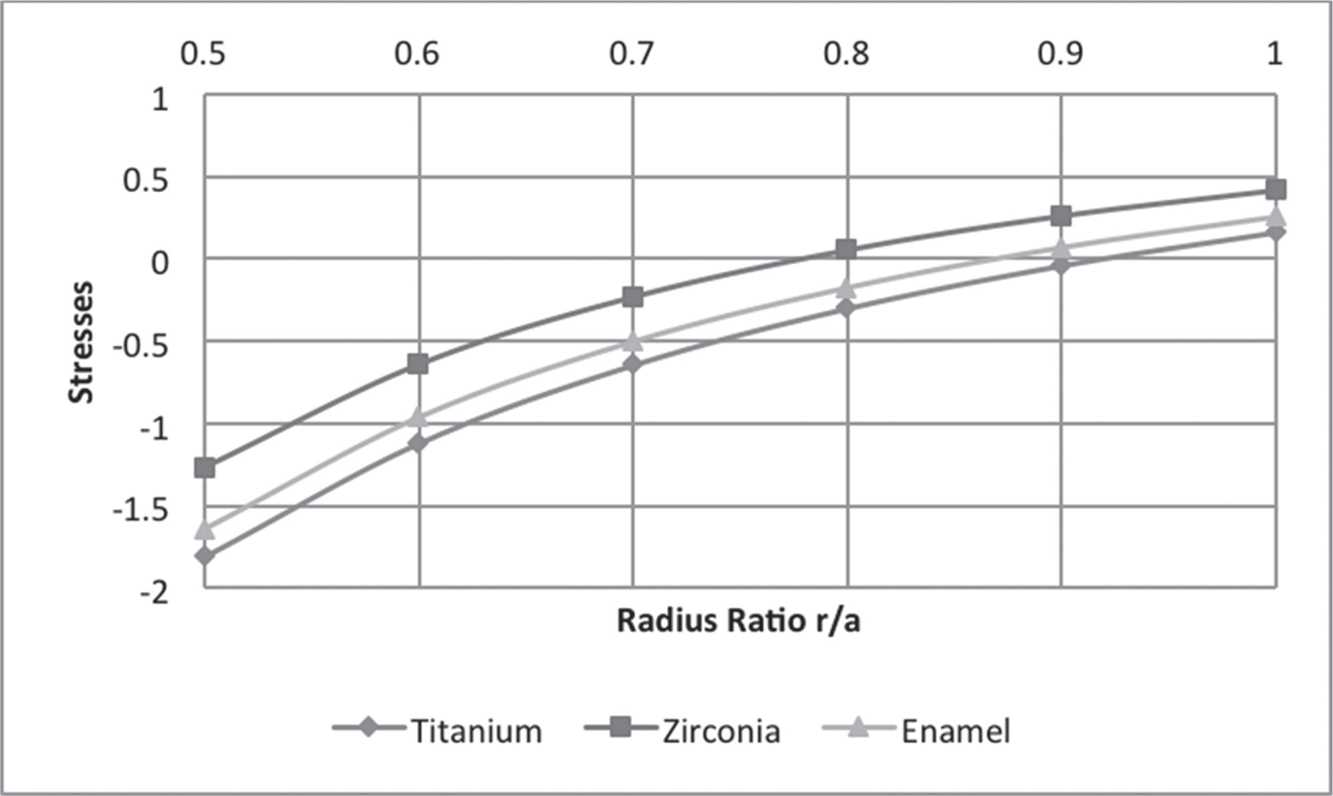
FIGURE 7.4 Circumferential stresses at initial yielding.

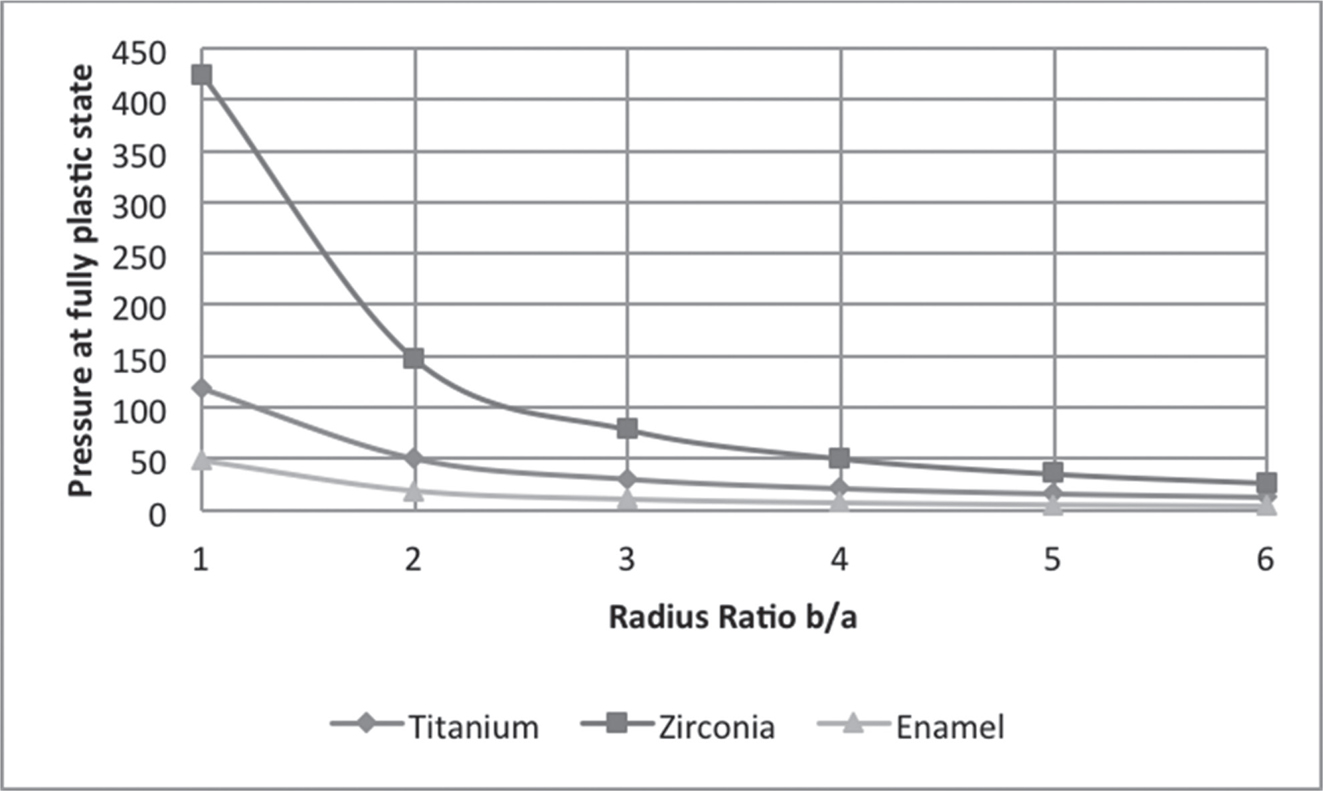
FIGURE 7.5 Pressure in the shell at fully plastic state for radius ratio R⁰.

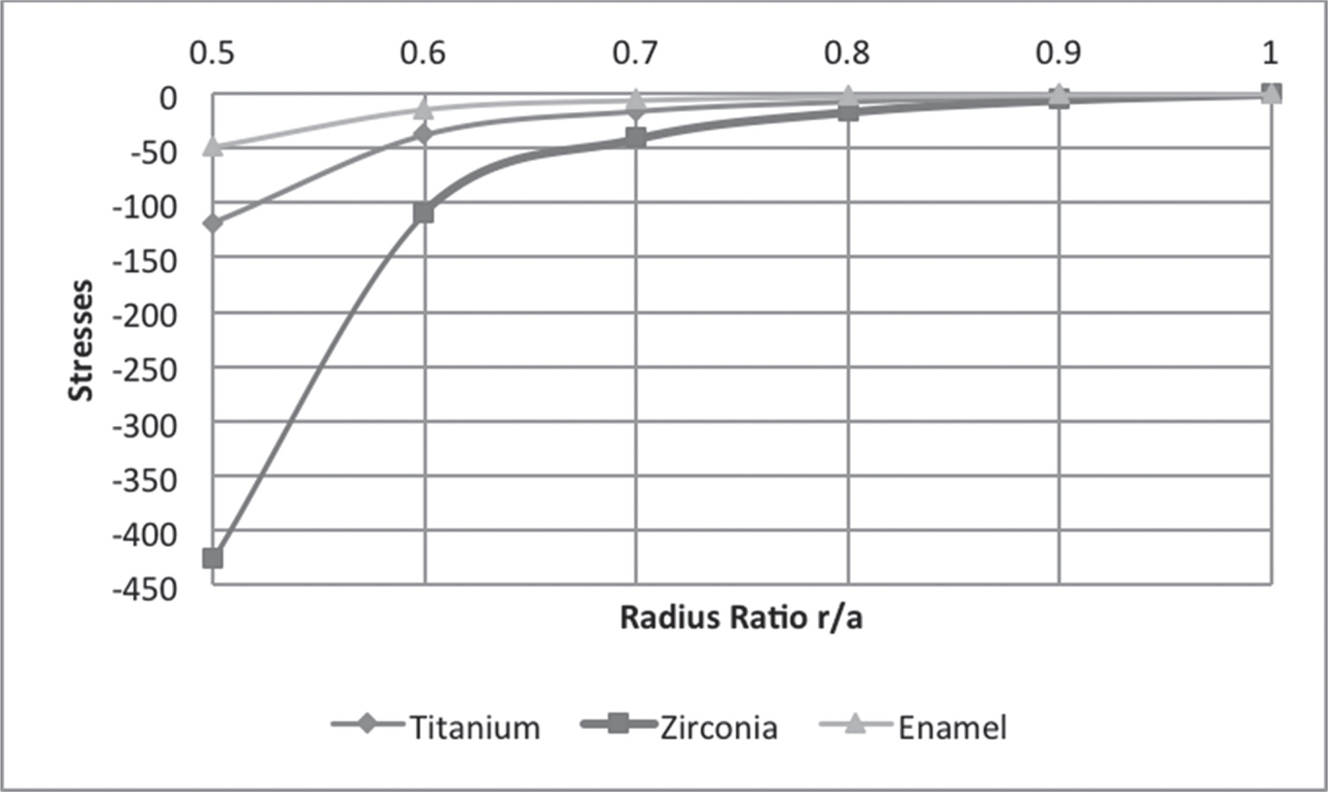
FIGURE 7.6 Radial stresses at fully plastic state.

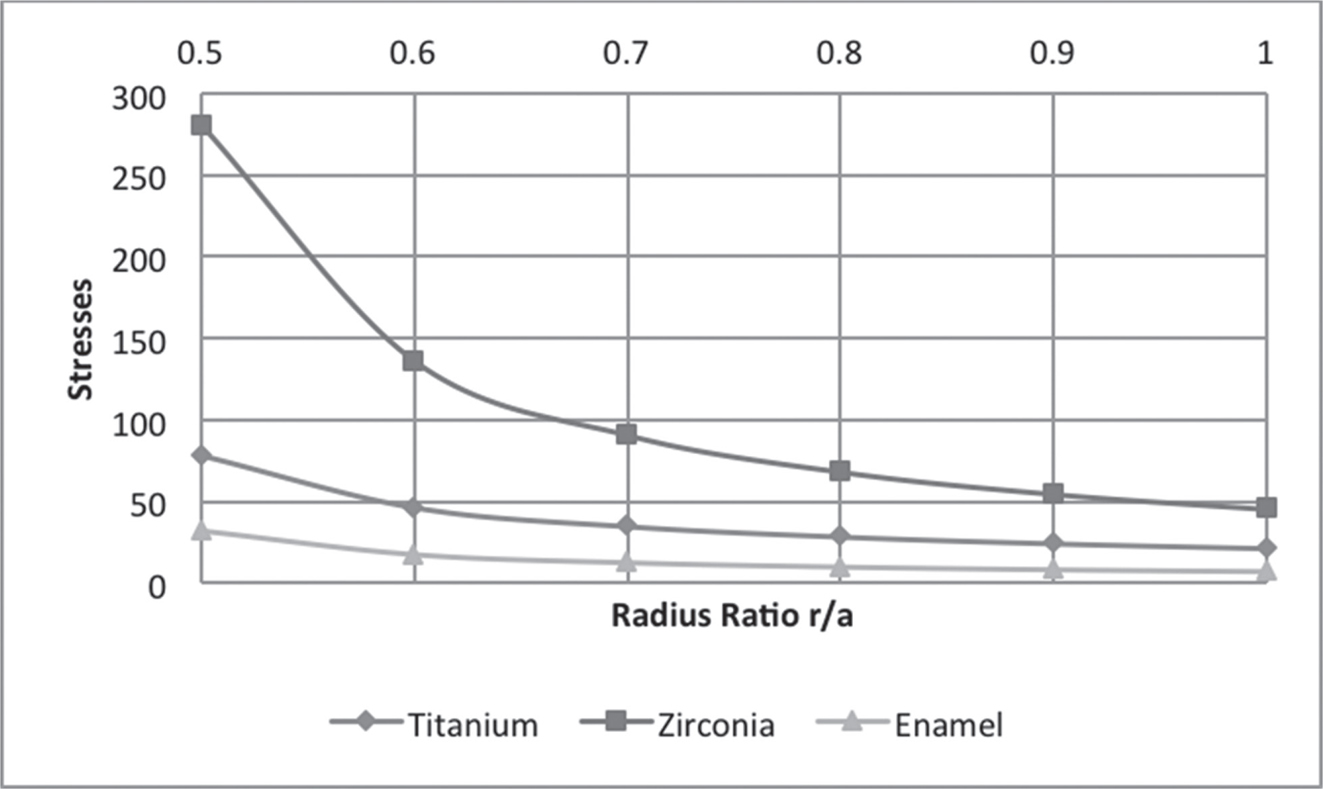
FIGURE 7.7 Circumferential stresses at fully plastic state.

7.5 CONCLUSIONS

The findings allow us to conclude that zirconia has a greater resemblance with enamel with the necessary elastic and plastic limit, which demonstrates considerable ability to suppress a crack growth. Varying values of pressure required for initial yielding and fully plastic state were calculated for various radius ratios depending on the geometry of the crown sample. Trends of the graphs were similar for enamel and HAP due to enamel’s composition. The significant difference between stress buildup at the inner and outer layer of the implant crown is observed by varying the radii ratios.

KEYWORDS