8.1 INTRODUCTION

The theory of elasticity is concerned with the study of elastic properties of a material having the property that once the deformation forces are removed, the material recovers back its original shape and size. But if the change of elastic properties of a material is due to the change in temperature, then the branch of applied mechanics dealing with this phenomenon is known as thermoelasticity. The deformations arising due to both mechanical and thermal causes were the reasons for the development of the subject of thermoelasticity. As the flow of heat through a body, causes heat conduction, stress, and strain in the body so thermoelasticity is a multi-field discipline governed by the interaction of a temperature deformation field.

If any thermodynamical changes occur in a homogeneous body in equilibrium due to the action of external loads, forces within the body, and non-uniform heating; then all such changes are concerned with the theory of Thermoelasticity. Due to such type of changes, the body undergoes deformation, thus causing stresses in the body and a rise in the body temperature. In the classical theory of thermoelasticity, the change of temperature being very small has not much effect and so the corresponding terms can be neglected. However, this is not true in such cases if the temperature undergoes a large and sudden change where the inertia term has to be considered in the equations of motion.

The nonlocal theory of thermoelasticity considers that the various physical quantities defined at a point are not just a function of the values of independent constitutive variables at that point only but a function of their values over the whole body. Thus, the nonlocal continuum field theories are concerned with the physics of material bodies in which the stress at any reference point within a continuous body not only depends on the strain at that point, but is having a significant influence due to the strains at all other points. So the nonlocal stress forces can be termed as remote action forces. Nonlocality is an essential characteristic in solid-state physics as nonlocal attractions of atoms are common. Nonlocal continuum theories can describe the material properties from microscopic scales to the size of the lattice parameter. So the nonlocal theory can satisfactorily explain some phenomena related to atomic scales.

The nonlocal theory in a way is just a generalization of the classical field theory. As: (i) the energy balance law is valid for the whole body, and (ii) the state of the body at a material point is considered to be attracted by all points of the body. This just means that a complete knowledge of the independent variables at all the points of the body is required to describe the state of the body at each point. Nonlocal effects are dominant in nature. So only, a nonlocal theory can provide the correct results where the classical theory fails. If the effects of strains at points other than the reference point are neglected, classical theory is recovered.

8.2 HISTORY AND RECENT ADVANCES IN THE CONCEPT OF NONLOCALITY

The theory of coupling of thermal and the strain fields gave rise to Coupled Theory of Thermoelasticity. Duhamel [1] derived the equations for the coupling between the strain and the temperature fields in an elastic medium, but the heat equation derived by him being parabolic gave an infinite speed of propagation for temperature. Biot [2] gave a satisfactory derivation of the heat conduction equation. Lord and Shulman [3] formulated a generalized dynamical theory of thermo-elasticity. According to this theory, the prediction is that the temperature travels with a finite speed due to the heat equation being hyperbolic.

The theory of nonlocal elasticity was developed by the contribution of many researchers. This theory is based on nonlocal effects i.e., the various physical quantities at a point are not a function of that point only but depend on their values over the whole body. Kroner [4] developed a continuum theory for long-range cohesive forces in elastic materials. He explained how the range effects can be important in materials having Vander Waals interactions as local theory gave a zero force. Edelen and Law [5] discussed a theory of nonlocal interactions and agreed to the concept of nonlocality as suggested by Kroner. Edelen et al. [6] discussed the consequences of the global postulate of energy balance and obtained the constitutive equations for the nonlinear theory. They called this nonlinear theory of nonlocal elasticity as protoelasticity.

Eringen and Edelen [7] developed the nonlocal elasticity theory via using the global balance laws and the second law of thermodynamics. This theory contains information about long-range forces of atoms as according to this theory the stress field at a particular point is affected due to the strain at all the other points of the body also. These are characterized by the presence of nonlocality residuals of fields (like body forces, internal energy, entropy, etc.). Balta and Suhubi [8] developed a new theory of nonlocal generalized thermoelasticity within the framework of the nonlocal continuum mechanics. The constitutive relations were obtained through the systematic use of the nonlocal version of the generalized thermodynamics and investigated thermal waves in rigid conductors.

Altan [9] studied the uniqueness in the linear theory of nonlocal elasticity. He concluded that under certain conditions the solutions of an initial-boundary value problem are unique. Wang and Dhaliwal [10] established a reciprocity relation and addressed some other issues addressing the nonlocal theory of micropolar elasticity to extend the concept of nonlocality further to other fields. Dhaliwal and Wang [11] provided more results on nonlocal thermoelasticity. Artan [12] compared the results of local and nonlocal elasticity theories by differentiating between the stress distributions of the local and the nonlocal theories to prove the superiority of the nonlocal theory.

The implications of the Eringen model of nonlocal elasticity theory were studied by Polizzotto [13]. He assumed an attenuation function and used it to further refine the theory. The attenuation function was supposed to be dependent on the geodetical distance replacing the Euclidean distance between material particles. He established the conditions for the uniqueness of the solution in the case of the nonlocal boundary value problem for infinitesimal displacements.

Eringen [14] presented a unified approach to the development of the basic field equations for nonlocal continuum field theories. He developed this theory for prevalent nonlocal intermolecular attractions in material bodies. In classical field theories, there exist a large number of problems falling outside their domain of applications. Some of the major deviations from the normal that confront with classical treatment are stress fields at the dislocation core, fracture of solids, short-wavelength behavior of elastic waves, etc.

Sharma and Ganti [15] described the size-dependent elastic stress state of inclusions in nonlocal media. Paola et al. [16] represented the mechanical based approach to three-dimensional nonlocal elasticity theories and proved the size dependence of the results. The model as proposed by them modeled the long-range forces as the central body forces and so for any element, the equilibrium is attained not just by contact forces at adjacent elements but also by long-range forces due to non-adjacent elements.

Ke and Wang [17] investigated the thermoelectric-mechanical vibration of the piezoelectric nanobeams-based on the nonlocal theory and Timoshenko beam theory. They discussed the influences of the nonlocal parameter, temperature change, external electric voltage, and axial force on the thermoelectric-mechanical vibration characteristics of the piezoelectric nanobeams in detail and found that the nonlocal effect is significant for the natural frequencies of the nanobeams. Khurana and Tomar [18] studied the propagation of plane longitudinal waves through an isotropic nonlocal micropolar elastic medium and showed that four dispersive waves and two sets of coupled transverse waves may propagate. As in Figure 8.1, they explained the variation of modulus of reflection coefficient with angle of incidence using local and nonlocal parameters. The solid curve denoted nonlocal micropolar solid and dotted denoted local micropolar solid.

Zenkour et al. [19] developed a generalized thermoelasticity theory with non-local deformation effects and dual-phase-lag or time-delay thermal effects to study the vibration of a nanobeam subjected to ramp-type heating. They analyzed nonlocal effects as in Figure 8.2; the transverse deflection distributions in the axial direction with different nonlocal ther-moelastic parameters were studied. The dotted line indicates the value at the points where nonlocal parameter is taken to be zero, while the other two lines indicate the values with a nonlocal parameter having nonzero values, i.e., 1 and 3.

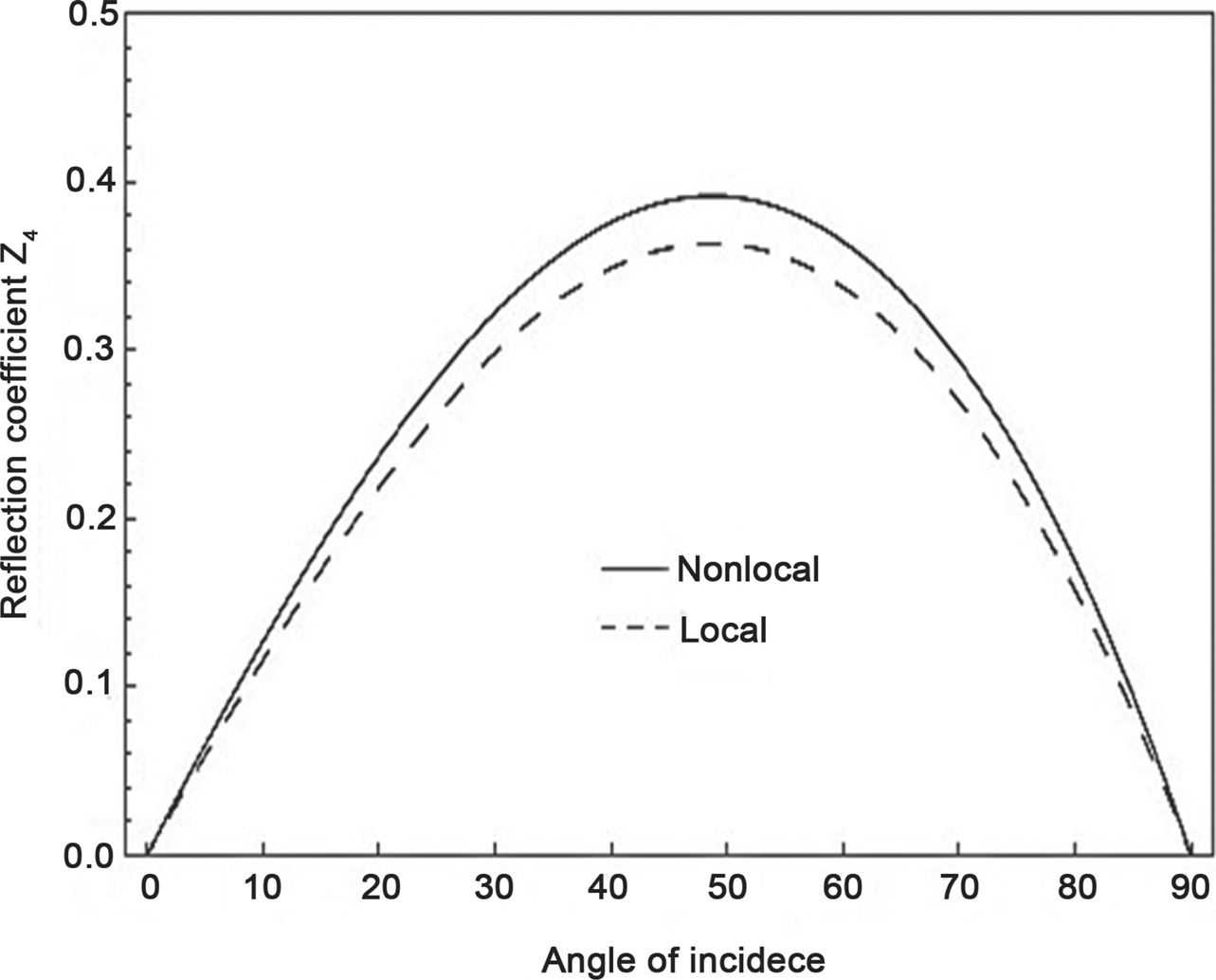
FIGURE 8.1 Variation of modulus of reflection coefficient with angle of incidence using local and nonlocal parameters.

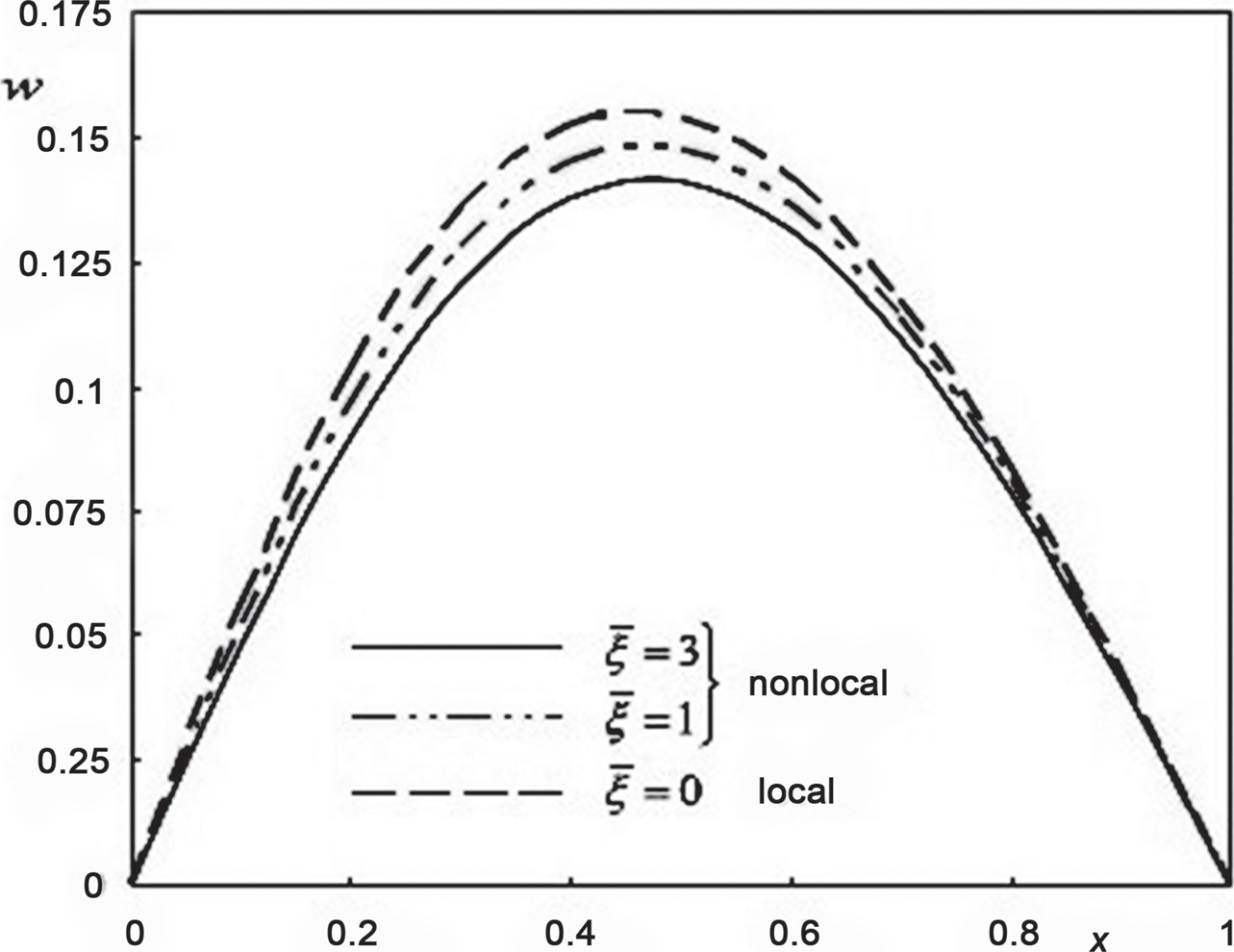
FIGURE 8.2 Transverse deflection distributions in the axial direction with different nonlocal thermoelastic parameters.

Salehipour et al. [20] gave a modified nonlocal elasticity theory stating that the strain tensor at all the neighboring points contributes to the imaginary nonlocal strain tensor at a particular point. The need for this theory arose as in the case of functionally graded materials (FGMs), the nonlocal theory of Eringen was not found to be worthy enough. They used a nonlocal strain tensor very similar to the stress tensor as used in nonlocal theory given by Eringen. This assumed strain tensor was used for obtaining the nonlocal stress tensor. Then, Vasiliev and Lurie [21] developed a new nonlocal generalized theory. Using a variational approach, they developed a new variant of nonlocal elasticity theory for generalized stresses by introducing high gradient equilibrium equations.

Jun Yu et al. [22] investigated the Buckling analysis of nanobeams with the aids of the size-dependent model, i.e., nonlocal thermoelasticity, and size effect of heat conduction. They adopted the Euler-Bernoulli beam and reformulated it within the nonlocal theory. Hayati et al. [23] analyzed the static and dynamic behavior of a curved single-walled carbon nanotube which is under twist-bending couple based on nonlocal theory. They used the nonlocal theory to model the mechanical behavior of the structure on a small scale. Togun [24] studied nonlinear vibrations of a Euler-Bernoulli nanobeam resting on an elastic foundation using nonlocal elasticity theory. Hamilton’s principle was employed to derive the governing equations and boundary conditions. The nonlinear equation of motion was obtained by including stretching of the neutral axis that introduces cubic nonlinearity into the equations.

Khurana and Tomar [25] studied the propagation of Rayleigh surface waves and explored the conditions for their existence. Singh et al. [26] studied the propagation of plane harmonic waves and derived the governing relations in nonlocal elastic solid with voids. Hosseini [27] developed a meshless method based on the generalized finite difference method for coupled thermoelasticity analysis. The Green-Naghditheory of the generalized coupled thermoelasticity and nonlocal Rayleigh beam theory were utilized for dynamic analysis of a micro/nanobeam resonator subjected to thermal shock loading. Zenkour [28] used a model of nonlocal thermoelasticity theory of Green and Naghdi without energy dissipation to consider the vibration behavior of a nano-machined resonator. He used nonlocality to bring in an internal length scale in the formulation and, thus, allowing for the interpretation of size effects. The governing frequency equation was given for nanobeams subjected to different boundary conditions.

Kaur et al. [29] derived dispersion relation and investigated the propagation of Rayleigh type surface wave in a nonlocal elastic solid. They studied the nonlocal effects in detail and their effects on the propagation of Rayleigh waves and continued the good work done by Khurana et al., Tomar et al., and Singh. A part of their research work can be elaborated as in Figure 8.3, where the variation of tilt with the nonlocality parameter is studied.

Bachher and Sarkar [30] postulated a new nonlocal theory of ther-moelasticity, which is based on Eringen’s nonlocal elasticity theory for thermoelastic materials with voids. A material needed to be classified according to its fractional and elastic nonlocality parameter by this theory. They studied the effects of nonlocality on various parameters such as temperature, displacement, stress, and change in volume fraction. For illustration, as in Figure 8.3, they studied the effect of the nonlocality parameter on dimensionless stress. It is clear from Figure 8.4, that there is a big effect of nonlocality on stress. Similarly, he proved identical results for other parameters too.

FIGURE 8.3 Variation of tilt with nonlocality parameter.

Lata [31] studied the reflection and refraction of plane waves in a layered medium of two semi-infinite nonlocal solids with the anisotropic thermoelastic medium as intermediate. She too depicted the nonlocal parameter effects graphically and proved that nonlocality is a significant parameter, which needs to be considered to get more accurate results.

8.3 CONCLUSION

The theory of elasticity and thermoelasticity are well established already. These are of wide interest in the fields where engineers, mathematicians,

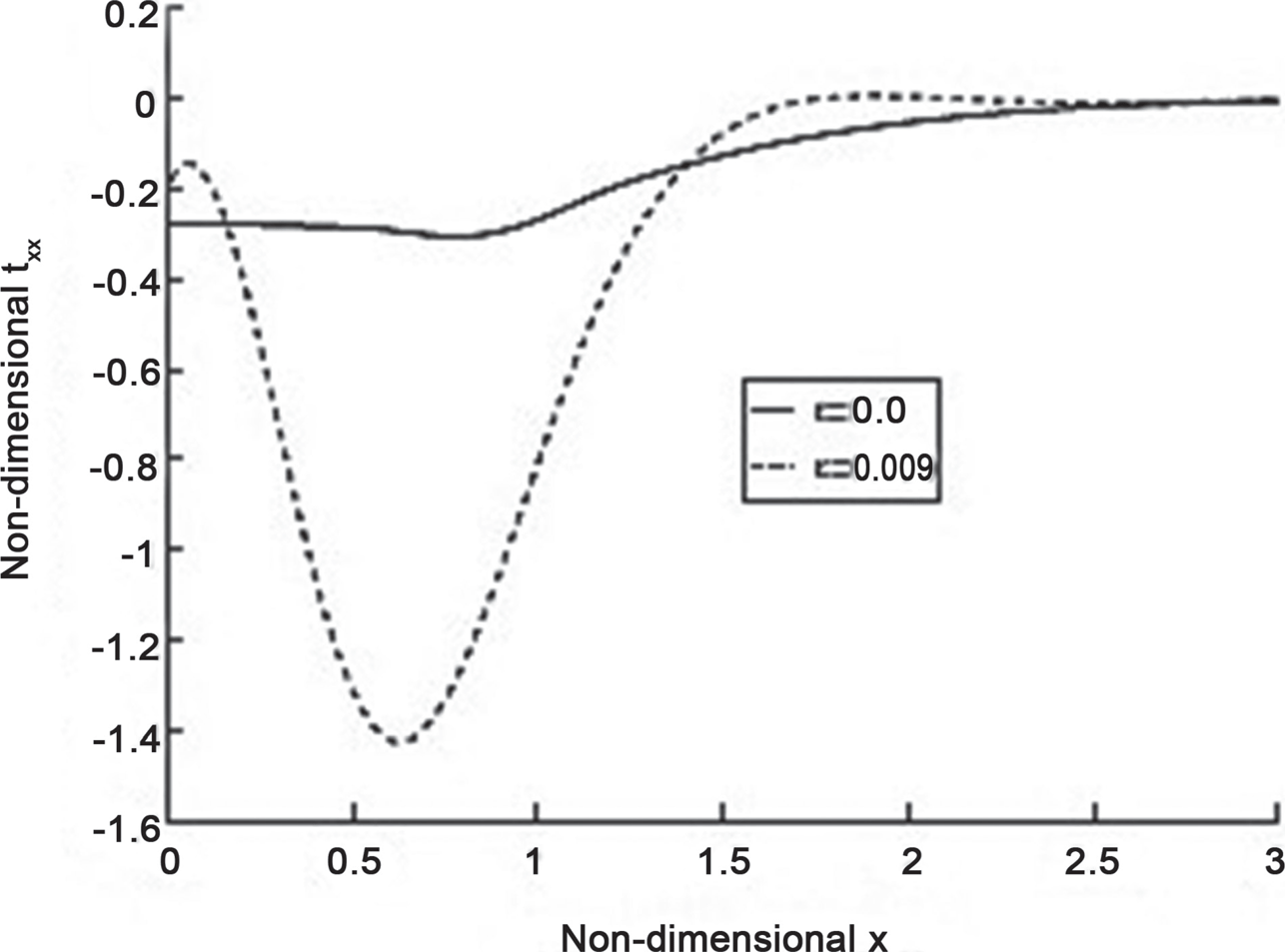
FIGURE 8.4 Effect of nonlocality parameter on dimensionless stress.

and physicists work together as these have a wider deal of applications in aeronautical engineering, nuclear physics, shipbuilding, in technologies of space vehicles and missiles, etc. As the use of the concept of nonlocality provides more refined and corrected results so it is causing more and more benefits to the subject of elasticity and thermoelasticity and thus helping in their overall development. Also, some of the well-established theories have been already refined using nonlocality and many more are to come yet. From the above, we can conclude that in the last two decades there have been great advances in the concept of nonlocality in elasticity and thermoelasticity. Many of the authors have already provided some astonishing results in the subject of thermoelasticity due to the use of nonlocality. But still, there is a lot to be done in the field of the nonlocal theory of thermoelasticity. This review chapter is a little effort to boost the researchers so that much more can be achieved in this field.

KEYWORDS